Đề thi vào 10 môn Toán Quảng Ngãi năm 2025

Đề bài

Bài 1. (2 điểm)

1. a) Thực hiện phép tính \(3\sqrt {25}  + \sqrt[3]{8}\).

b) Rút gọn biểu thức \(Q = 1 + \frac{{x - 1}}{{\sqrt x  + 1}}\), với mọi \(x \ge 0\).

2. Cho hàm số \(y = {x^2}\) có đồ thị (P).

a) Vẽ đồ thị (P).

b) Tìm tọa độ các giao điểm của (P) và đường thẳng (d): \(y =  - x + 2\).

Bài 2. (2,5 điểm)

1. Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{3x + 2y = 8}\\{2x - y = 3}\end{array}} \right.\).

2. Chứng minh phương trình \({x^2} - 12x + 35 = 0\) có hai nghiệm phân biệt \({x_1},{x_2}\). Không giải phương trình, hãy tính giá trị của biểu thức \(A = x_1^2 + x_2^2 + {x_1}{x_2}\).

3. Một xe ô tô và một xe máy khởi hành cùng một lúc từ A để đi đến B với quãng đường AB dài 160 km. Do vận tốc của xe ô tô lớn hơn vận tốc của xe máy là 10 km/h nên xe ô tô đến B trước xe máy 48 phút. Tính vận tốc của mỗi xe.

Bài 3. (1 điểm) Một công ty du lịch cần chọn 3 trong 4 địa điểm là Lý Sơn (LS), Hội An (HA), Phú Yên (PY), Quy Nhơn (QN) để tổ chức các chuyến du lịch nhân dịp lễ Quốc Khánh 2-9. Công ty tiến hành khảo sát 30 gia đình. Kết quả khảo sát được liệt kê dưới đây:

a) Hãy lập bảng tần số cho kết quả khảo sát trên.

b) Ba địa điểm được chọn nhiều nhất theo kết quả khảo sát trên được công ty chọn để tổ chức các chuyến đi. Gia đình bạn Long và gia đình bạn Phượng mỗi gia đình chọn ngẫu nhiên một trong ba địa điểm đó để đi du lịch. Tính xác suất để cả hai gia đình cùng chọn một địa điểm.

Bài 4. (3,5 điểm)

1. Một thùng nhựa dạng hình trụ có bán kính đáy 10 cm và chiều cao 30 cm.

a) Tính thể tích của thùng nhựa.

b) Bác Hoa mua một thúng muối vun đầy, cái thúng có dạng nửa hình cầu với đường kính 48 cm, phần muối vun lên có dạng hình nón với chiều cao 14 cm (hình vẽ bên). Bác Hoa cần phải sử dụng ít nhất bao nhiêu thùng nhựa như trên để đựng hết lượng muối đã mua.

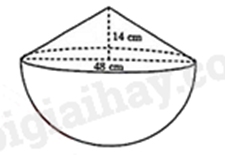
(Bỏ qua bề dày của thùng nhựa và thúng)

2. Cho đường tròn (O) đường kính AB bằng 2R. Gọi D là trung điểm của OB, vẽ đường thẳng a qua D và vuông góc với AB. Trên đường thẳng a, lấy điểm C nằm ngoài đường tròn (O). Hai đường thẳng AC, BC cắt đường tròn (O) lần lượt tại E, F (với E khác A và F khác B ). Gọi H là giao điểm của AF và CD.

a) Chứng minh tứ giác BDHF nội tiếp.

b) Chứng minh \(AE \cdot AC = 3{R^2}\).

c) Vẽ EI vuông góc với AB tại I, cho biết \(EI = 8\;{\rm{cm}}\) và \(R = 10\;{\rm{cm}}\). Đường thẳng qua E cắt hai tia DA, DC lần lượt tại M, N. Đặt \(IM = x\;{\rm{cm}}\), tính DN theo x và tìm x để diện tích tam giác DMN nhỏ nhất.

Bài 5. (1 điểm) Ở một giải vô địch bóng đá, có 5 đội bóng tham gia là A, B, C, D, E. Các đội thi đấu theo thể thức vòng tròn một lượt (mỗi đội thi đấu đúng một trận với các đội còn lại). Trong mỗi trận đấu, đội thua không có điểm, hai đội hòa nhau mỗi đội được một điểm và đội thắng được ba điểm. Khi kết thúc giải, các đội A, B, C, D, E có số điểm tương ứng là 8, 6, 4, 3, 5. Khi đó, có bao nhiêu trận đấu được phân định thắng thua và kết quả của hai trận đấu A gặp C và B gặp D là gì? Vì sao?

----HẾT----

Lời giải

Bài 1. (2 điểm)

1. a) Thực hiện phép tính \(3\sqrt {25}  + \sqrt[3]{8}\).

b) Rút gọn biểu thức \(Q = 1 + \frac{{x - 1}}{{\sqrt x  + 1}}\), với mọi \(x \ge 0\).

2. Cho hàm số \(y = {x^2}\) có đồ thị (P).

a) Vẽ đồ thị (P).

b) Tìm tọa độ các giao điểm của (P) và đường thẳng (d): \(y =  - x + 2\).

Lời giải:

1.

a) \(3\sqrt {25}  + \sqrt[3]{8} = 3.5 + 2 = 17\)

b) \(Q = 1 + \frac{{x - 1}}{{\sqrt x  + 1}}\) (với \(x \ge 0\))

\( = \frac{{\sqrt x  + 1}}{{\sqrt x  + 1}} + \frac{{x - 1}}{{\sqrt x  + 1}}\)

\( = \frac{{x + \sqrt x }}{{\sqrt x  + 1}}\)

\( = \frac{{\sqrt x \left( {\sqrt x  + 1} \right)}}{{\sqrt x  + 1}}\)

\( = \sqrt x \).

Vậy \(Q = \sqrt x \) với \(x \ge 0\).

2.

a) Ta có bảng giá trị sau:

Đồ thị hàm số là đường cong parabol đi qua các điểm:

\(O\,\left( {0;0} \right);A\left( { - 2;4} \right);\,\,B\left( { - 1;1} \right);C\left( {1;1} \right);\,\,D\left( {2;4} \right)\)

Hệ số \(a = 1 > 0\) nên parabol có bề cong hướng lên. Đồ thị hàm số nhận Oy làm trục đối xứng.

Ta vẽ được đồ thị hàm số \(y = {x^2}\) như sau:

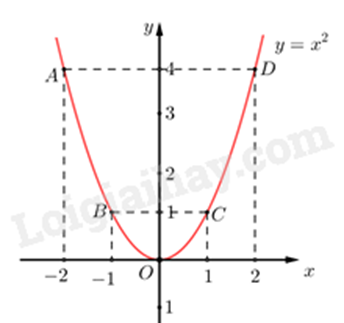
b) Xét phương trình hoành độ giao điểm:

\({x^2} =  - x + 2\)

\({x^2} + x - 2 = 0\) (*)

Xét phương trình (*) có a = 1, b = 1, c = -2:

Ta có \(a + b + c = 1 + 1 + ( - 2) = 0\) nên phương trình (*) có hai nghiệm phân biệt:

\({x_1} = 1\); \({x_2} =  - 2\).

Vậy (d) giao với (P) tại hai điểm lần lượt có hoành độ là \({x_1} = 1\), \({x_2} =  - 2\).

Với \({x_1} = 1\), ta có \({y_1} = {x_1}^2 = {1^2} = 1\).

Với \({x_2} =  - 2\), ta có \({y_2} = {x_2}^2 = {( - 2)^2} = 4\).

Vậy các giao điểm của (P) và đường thẳng (d) là C(1;1) và A(-2;4).

Bài 2. (2,5 điểm)

1. Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{3x + 2y = 8}\\{2x - y = 3}\end{array}} \right.\).

2. Chứng minh phương trình \({x^2} - 12x + 35 = 0\) có hai nghiệm phân biệt \({x_1},{x_2}\). Không giải phương trình, hãy tính giá trị của biểu thức \(A = x_1^2 + x_2^2 + {x_1}{x_2}\).

3. Một xe ô tô và một xe máy khởi hành cùng một lúc từ A để đi đến B với quãng đường AB dài 160 km. Do vận tốc của xe ô tô lớn hơn vận tốc của xe máy là 10 km/h nên xe ô tô đến B trước xe máy 48 phút. Tính vận tốc của mỗi xe.

Lời giải:

1. \(\left\{ {\begin{array}{*{20}{l}}{3x + 2y = 8}\\{2x - y = 3}\end{array}} \right.\)

\(\left\{ {\begin{array}{*{20}{l}}{3x + 2y = 8}\\{4x - 2y = 6}\end{array}} \right.\)

\(\begin{array}{l}\left\{ {\begin{array}{*{20}{l}}{7x = 14}\\{4x - 2y = 6}\end{array}} \right.\\\left\{ {\begin{array}{*{20}{l}}{x = 2}\\{4x - 2y = 6}\end{array}} \right.\end{array}\)

\(\left\{ {\begin{array}{*{20}{l}}{x = 2}\\{4.2 - 2y = 6}\end{array}} \right.\)

\(\begin{array}{l}\left\{ {\begin{array}{*{20}{l}}{x = 2}\\{2y = 2}\end{array}} \right.\\\left\{ {\begin{array}{*{20}{l}}{x = 2}\\{y = 1}\end{array}} \right.\end{array}\)

Vậy hệ phương trình có nghiệm \(\left( {x;y} \right) = \left( {2;1} \right).\)

2. Phương trình \({x^2} - 12x + 35 = 0\) có \(\Delta  = {\left( { - 12} \right)^2} - 4.35 = 4 > 0\) nên phương trình có hai nghiệm phân biệt \({x_1},{x_2}\).

Theo Viete, ta có \(\left\{ \begin{array}{l}{x_1} + {x_2} = 12\\{x_1}{x_2} = 35\end{array} \right.\)

Ta có

\(\begin{array}{l}A = x_1^2 + x_2^2 + {x_1}{x_2}\\A = x_1^2 + 2{x_1}{x_2} + x_2^2 + {x_1}{x_2} - 2{x_1}{x_2}\\A = {\left( {{x_1} + {x_2}} \right)^2} - {x_1}{x_2}\\A = {12^2} - 35\\A = 109\end{array}\)

Vậy giá trị của biểu thức A là 109.

3. Gọi vận tốc của ô tô là \(x\) (km/h), \(x > 10\)

Khi đó vận tốc của xe máy là \(x - 10\) (km/h)

Thời gian ô tô đi hết quãng đường là \(\frac{{160}}{x}\) (giờ)

Thời gian xe máy đi hết quãng đường là \(\frac{{160}}{{x - 10}}\) (giờ)

Xe ô tô đến trước xe máy 48 phút = \(\frac{4}{5}\) giờ.

Ta có phương trình: \(\frac{{160}}{{x - 10}} - \frac{{160}}{x} = \frac{4}{5}\)

\(\begin{array}{l}\frac{{160}}{{x - 10}} - \frac{{160}}{x} = \frac{4}{5}\\160.5x - 160.5\left( {x - 10} \right) = 4x\left( {x - 10} \right)\\4{x^2} - 40x - 8000 = 0\end{array}\)

Giải phương trình \(4{x^2} - 40x - 8000 = 0\) ta được \(x = 50\) (tmđk) và \(x =  - 40\) (loại).

Vậy vận tốc của ô tô là 50 km/h và vận tốc của xe máy là 40 km/h.

Bài 3. (1 điểm) Một công ty du lịch cần chọn 3 trong 4 địa điểm là Lý Sơn (LS), Hội An (HA), Phú Yên (PY), Quy Nhơn (QN) để tổ chức các chuyến du lịch nhân dịp lễ Quốc Khánh 2-9. Công ty tiến hành khảo sát 30 gia đình. Kết quả khảo sát được liệt kê dưới đây:

a) Hãy lập bảng tần số cho kết quả khảo sát trên.

b) Ba địa điểm được chọn nhiều nhất theo kết quả khảo sát trên được công ty chọn để tổ chức các chuyến đi. Gia đình bạn Long và gia đình bạn Phượng mỗi gia đình chọn ngẫu nhiên một trong ba địa điểm đó để đi du lịch. Tính xác suất để cả hai gia đình cùng chọn một địa điểm.

Lời giải:

a) Bảng tần số cho kết quả khảo sát trên là:

b) Ba địa điểm được chọn nhiều nhất là Lý Sơn, Hội An và Quy Nhơn.

Các kết quả có thể khi gia đình bạn Long và gia đình bạn Phương chọn một trong ba địa điểm trên là:

(LS, LS); (LS; HA); (LS, QN); (HA, LS); (HA, HA); (HA, QN); (QN, LS); (QN, HA); (QN, QN).

Có 9 kết quả có thể khi gia đình bạn Long và gia đình bạn Phương chọn một địa điểm để đi du lịch.

Có 3 kết quả hai gia đình cùng chọn một địa điểm, đó là: (LS, LS); (HA, HA); (QN, QN).

Xác suất để cả hai gia đình cùng chọn một địa điểm là: \(\frac{3}{9} = \frac{1}{3}\).

Bài 4. (3,5 điểm)

1. Một thùng nhựa dạng hình trụ có bán kính đáy 10 cm và chiều cao 30 cm.

a) Tính thể tích của thùng nhựa.

b) Bác Hoa mua một thúng muối vun đầy, cái thúng có dạng nửa hình cầu với đường kính 48 cm, phần muối vun lên có dạng hình nón với chiều cao 14 cm (hình vẽ bên). Bác Hoa cần phải sử dụng ít nhất bao nhiêu thùng nhựa như trên để đựng hết lượng muối đã mua.

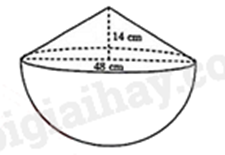
(Bỏ qua bề dày của thùng nhựa và thúng)

2. Cho đường tròn (O) đường kính AB bằng 2R. Gọi D là trung điểm của OB, vẽ đường thẳng a qua D và vuông góc với AB. Trên đường thẳng a, lấy điểm C nằm ngoài đường tròn (O). Hai đường thẳng AC, BC cắt đường tròn (O) lần lượt tại E, F (với E khác A và F khác B ). Gọi H là giao điểm của AF và CD.

a) Chứng minh tứ giác BDHF nội tiếp.

b) Chứng minh \(AE \cdot AC = 3{R^2}\).

c) Vẽ EI vuông góc với AB tại I, cho biết \(EI = 8\;{\rm{cm}}\) và \(R = 10\;{\rm{cm}}\). Đường thẳng qua E cắt hai tia DA, DC lần lượt tại M, N. Đặt \(IM = x\;{\rm{cm}}\), tính DN theo x và tìm x để diện tích tam giác DMN nhỏ nhất.

Lời giải:

1.

a) Thể tích của thùng nhựa: \(V = \pi {R^2}h\)

\(V = \pi {.10^2}.30 = 3000.\pi \,\left( {c{m^3}} \right)\)

b) Chia thúng muối thành hai phần:

Bán kính thúng là: \(48:2 = 24\left( {cm} \right)\)

Thể tích thúng muối là: \({V_1} = \frac{1}{2}.\frac{4}{3}\pi .{R^3} = \frac{1}{2}.\frac{4}{3}.\pi .{\left( {24} \right)^3} = 9216\pi \left( {c{m^3}} \right)\)

Phần muối vun lên có thể tích là: \({V_2} = \frac{1}{3}\pi .{R^2}.h = \frac{1}{3}\pi {.24^2}.14 = 2688\pi \left( {c{n^3}} \right)\)

Thể tích muối: \(V = {V_1} + {V_2} = 9216\pi  + 2688\pi  = 11904\pi \left( {c{m^3}} \right)\)

Số thùng nhựa cần để chứa hết muối là: \(\frac{{11904\pi }}{{3000\pi }} = 3,968\)

Vậy cần ít nhất 4 thùng mới đựng đủ số muối trên.

2.

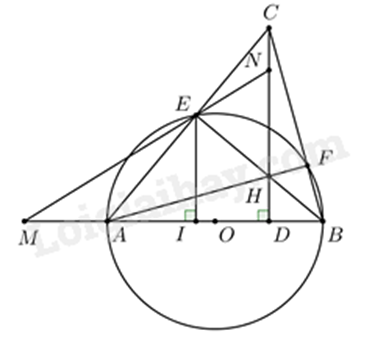
a) Do \(E,F \in \left( O \right)\) nên \(\angle AEB = \angle AFB = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)

Khi đó \(\Delta BHF\) vuông tại F nên B, F, H cùng thuộc đường tròn đường kính BH

Và \(\Delta HDB\) vuông tại D nên H, D, B cùng thuộc đường tròn đường kính BH

Vậy B, D, H, F cùng thuộc đường tròn đường kính BH hay tứ giác BDHF nội tiếp.

b) Xét \(\Delta AEB\) và \(\Delta ADC\) có

\(\angle DAC\) là góc chung

\(\angle AEB = \angle ADC\left( { = 90^\circ } \right)\)

Suy ra $\Delta AEB\backsim \Delta ADC\left( g.g \right)$

Suy ra \(\frac{{AE}}{{AD}} = \frac{{AB}}{{AC}}\) hay \(AE.AC = AD.AB\)

Do D là trung điểm của OB nên \(OD = \frac{1}{2}OB = \frac{1}{2}R\) suy ra

\(AD = OA + OD = R + \frac{1}{2}R = \frac{3}{2}R\)

Suy ra \(AE.AC = AD.AB = \frac{3}{2}R.2R = 3{R^2}\)

c) Ta có \(\angle EAI = \angle IEB\) (do cùng cộng với \(\angle AEI\) bằng \(90^\circ \))

Suy ra $\Delta AEI\backsim \Delta EBI\left( g.g \right)$. Khi đó \(\frac{{IE}}{{IB}} = \frac{{IA}}{{IE}}\) hay \(I{E^2} = IA.IB\)

Suy ra \(IA.IB = {8^2} = 64\)

Mà \(IA + IB = AB = 2.10 = 20\)

Nên độ dài \(IA,IB\) là nghiệm của phương trình \({X^2} - 20X + 64 = 0\)

Giải phương trình ta được \(X = 16\) và \(X = 4\)

Vậy \(IA = 4\) cm và \(IB = 16\)cm (Do \(IA < IB\))

Do \(IM = x\) nên \(MA = IM - IA = x - 4\) (cm)

Suy ra \(MD = IM + ID = x + IB - DB = x + 16 - 5 = x + 11\) (cm)

Ta có \(EI\parallel DN\) (do cùng vuông góc với AB) nên \(\frac{{MI}}{{MD}} = \frac{{EI}}{{ND}}\)

Suy ra \(\frac{8}{{ND}} = \frac{x}{{x + 11}}\) hay \(ND = \frac{{8\left( {x + 11} \right)}}{x}\) (cm)

Khi đó diện tích tam giác DMN là

\(S = \frac{1}{2}DM.DN = \frac{1}{2}\left( {x + 11} \right).\frac{{8\left( {x + 11} \right)}}{x} = 4.\frac{{{{\left( {x + 11} \right)}^2}}}{x}\) cm²

Ta có

\(\frac{{4{{\left( {x + 11} \right)}^2}}}{x} = 4.\frac{{{x^2} + 22x + 121}}{x} = 4.\left( {x + \frac{{121}}{x} + 22} \right) \ge 4.\left( {2\sqrt {x.\frac{{121}}{x}}  + 22} \right) = 176\) (Áp dụng bất đẳng thức Cauchy). Dấu bằng có khi \(x = \frac{{121}}{x}\) hay \(x = 11\)

Vậy \(x = 11\) thì diện tích tam giác DMN nhỏ nhất.

Bài 5. (1 điểm) Ở một giải vô địch bóng đá, có 5 đội bóng tham gia là A, B, C, D, E. Các đội thi đấu theo thể thức vòng tròn một lượt (mỗi đội thi đấu đúng một trận với các đội còn lại). Trong mỗi trận đấu, đội thua không có điểm, hai đội hòa nhau mỗi đội được một điểm và đội thắng được ba điểm. Khi kết thúc giải, các đội A, B, C, D, E có số điểm tương ứng là 8, 6, 4, 3, 5. Khi đó, có bao nhiêu trận đấu được phân định thắng thua và kết quả của hai trận đấu A gặp C và B gặp D là gì? Vì sao?

Lời giải:

Có 5 đội bóng nên sẽ có tất cả 10 trận đấu gồm các trận đấu là \(A - B;A - C,A - D,A - E,B - C,B - D,B - E,C - D,C - E,D - E\)

Mỗi trận sẽ có tổng cộng 3 điểm nếu có thắng thua, và 2 điểm nếu hòa nên tổng điểm các đội là

\(A + B + C + D + E = 8 + 6 + 4 + 3 + 5 = 26\) điểm

Gọi \(x\) là số trận phân định thắng hoặc thua và y là số trận hoà \(\left( {x,y \in \mathbb{N},x,y < 10} \right)\)

Mỗi trận thắng - thua có 3 điểm, hòa có 2 điểm ⇒ tổng điểm từ tất cả trận là \(3x + 2y = 26\)

Khi đó ta có hệ \(\left\{ \begin{array}{l}x + y = 10\\3x + 2y = 26\end{array} \right.\)

Giải hệ phương trình ta được \(x = 6\) và \(y = 4\) tức là có tất cả 6 trận thắng hoặc thua và 4 trận hoà.

Do đội A được 8 điểm nên A thắng 2 trận và hoà 2 trận

Đội E được 5 điểm nên E thắng 1, hoà 2, thua 1 trận

Do D được 3 điểm nên D thắng 1, thua 3 hoặc D hoà 3 thua 1

Đội B được 6 điểm nên B thắng 2, hoà 0, thua 2 hoặc B thắng 1 hoà 3, thua 0

Đội C được 4 điểm nên C hoà 4 hoặc C thắng 1, hoà 1, thua 2

TH1: Nếu C hoà 4 trận thì B thắng 1 hoà 3, thua 0 và D hoà 3 thua 1

Mà B không thắng A nên B thua A => mâu thuẫn với B thua 0 trận nên vô lý

TH2: Ta có C thắng 1, hoà 1, thua 2.

     A thắng 2 trận và hoà 2 trận

     E thắng 1, hoà 2, thua 1 trận

KN1: Vậy B phải thắng 1 hoà 3, thua 0 thì đủ 4 trận hoà nên D không được hoà hay D thắng 1, thua 3

- Nếu B thắng A thì A có 1 trận thua nên vô lý => B Thua A => vô lý vì B không có trận thua

- Nếu B thắng C thì B hoà A, B hoà D => vô lý vì D không hoà

- Nếu B thắng E thì B hoà A, C, D => vô lý vì D không có trận hoà

=> Vậy B phải thắng D. Khi đó B hoà A, hoà C, hoà E.

Giả sử A hoà C thì C có 2 trận hoà => mâu thuẫn vậy A thắng C

Kết luận vậy A thắng C và B thắng D.

KN2: Nếu B thắng 2, hoà 0, thua 2 thì có 5 điểm hoà của 2 đội suy ra D phải hoà 3 thua 1

- Nếu D thua A, C hoặc E thì D hoà B=> vô lý vì B không có trận hoà

Vậy D phải thua B. Tức là D hoà A, C, E.

Vì C hoà D nên C thắng A thì vô lý vì A không có trận thua nên A phải thắng C

Kết luận vậy A thắng C và B thắng D.

Vậy A luôn luôn phải thắng C bà B luôn thắng D.