Đề thi vào 10 môn Toán Phú Yên năm 2025

Đề bài

I. TRẮC NGHIỆM (3,00 điểm)

Học sinh chọn một phương án đúng nhất ở mỗi câu và viết phương án chọn vào bài làm (Ví dụ: Câu 1: A, Câu 2: B, Câu 3: D...).

Câu 1: Biểu thức nào sau đây có giá trị khác với các biểu thức còn lại?

A. \(\sqrt 9 \).

B. \({( - \sqrt 3 )^2}\).

C. \(\sqrt {{{( - 3)}^2}} \).

D. \( - {(\sqrt 3 )^2}\).

Câu 2: Cho bất đẳng thức \(a > b\). Kết luận nào sau đây là không đúng?

A. \(3a > 3b\).

B. \(a - 1 < b - 1\).

C. \(a + 1 > b + 1\).

D. \( - 3a <  - 3b\).

Câu 3: Số nào sau đây không phải là một nghiệm của bất phương trình \(5x - 6 < 0\)?

A. \(\frac{5}{6}\).

B. \( - \frac{5}{6}\).

C. \(\frac{6}{5}\).

D. \( - \frac{6}{5}\).

Câu 4: Cặp số \(\left( {x;y} \right)\) nào sau đây là nghiệm của hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{3x - y = 1}\\{ - x + y = 1}\end{array}} \right.\)?

A. \(\left( {1;2} \right)\).

B. \(\left( {0; - 1} \right)\).

C. \(\left( {0;1} \right)\).

D. \(\left( {2;1} \right)\).

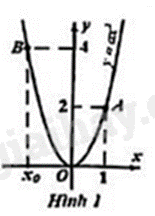
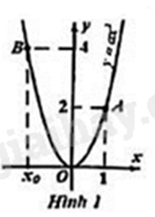
Câu 5: Giả sử đồ thị của hàm số \(y = a{x^2}\) là parabol như Hình 1. Giá trị của \({x_0}\) bằng

A. \(2\).

B. \(\sqrt 3 \).

C. \( - 1,5\).

D. \( - \sqrt 2 \).

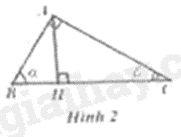
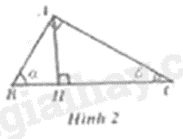
Câu 6: Tam giác \(ABC\) vuông tại \(A\) có đường cao \(AH\) (Hình 2). Khẳng định nào sau đây sai?

A. \({\rm{sin}}\alpha  = \frac{{AC}}{{BC}}\).

B. \({\rm{cos}}\alpha  = \frac{{BH}}{{BA}}\).

C. \({\rm{tan}}\beta  = \frac{{AB}}{{AC}}\).

D. \({\rm{cot}}\beta  = \frac{{AC}}{{AH}}\).

Câu 7: Tâm đường tròn nội tiếp tam giác là giao điểm của ba đường nào trong tam giác đó?

A. Đường phân giác.

B. Đường trung trực.

C. Đường cao.

D. Đường trung tuyến.

Câu 8: Một tam giác vuông có hai cạnh góc vuông lần lượt là \(5\) cm và \(12\) cm. Bán kính của đường tròn ngoại tiếp tam giác vuông đó bằng

A. \(8,5\) cm.

B. \(6,5\) cm.

C. \(13\) cm.

D. \(17\) cm.

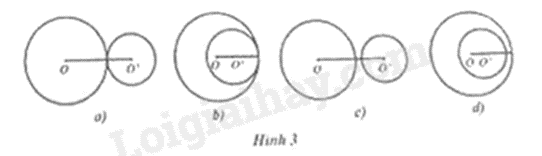
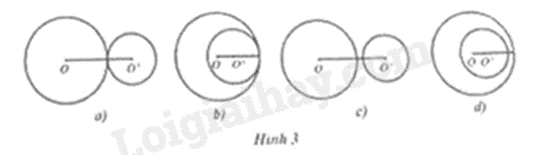
Câu 9: Mỗi hình a), b), c), d) trên Hình 3 là hai đường tròn phân biệt \(\left( {O;R} \right)\) và \(\left( {O';R'} \right)\). Hình nào có đoạn nối tâm và hai bán kính thỏa mãn \(OO' > R + R'\)?

A. Hình 3a).

B. Hình 3b).

C. Hình 3c).

D. Hình 3d).

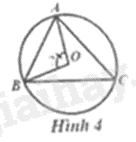
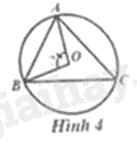
Câu 10: Cho tam giác \(ABC\) có \(\widehat {BAC} = 70^\circ \); \(\widehat {ABC} = 60^\circ \) nội tiếp đường tròn tâm \(O\) (Hình 4). Số đo của góc \(\widehat {AOB}\) bằng

A. \(50^\circ \).

B. \(100^\circ \).

C. \(120^\circ \).

D. \(140^\circ \).

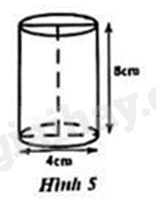
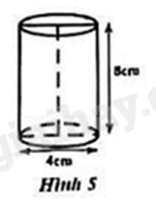
Câu 11: Thể tích của một hình trụ có đường kính đáy bằng 4 cm và chiều cao bằng 8 cm (Hình 5) là

A. \(64\pi c{m^3}\)

B. \(32\pi c{m^3}\)

C. \(\frac{{64\pi }}{3}c{m^3}\)

D. \(\frac{{32\pi }}{3}c{m^3}\)

Câu 12: Gieo đồng thời hai con xúc xắc cân đối, đồng chất. Xác suất của biến cố “tích của hai số chấm xuất hiện trên hai con xúc xắc bằng 7” là

A. 0

B. \(\frac{1}{{12}}\)

C. \(\frac{1}{7}\)

D. \(\frac{1}{6}\)

II. TỰ LUẬN (7,00 điểm)

Câu 13: (1,50 điểm)
1) Rút gọn biểu thức \(A = \sqrt {{{(\sqrt 3  - 2)}^2}}  - \frac{3}{{\sqrt 3 }} + \sqrt {12} \).
2) Cho phương trình bậc hai (ẩn \(x\)): \(2{x^2} + bx - 3 = 0\).
a) Chứng tỏ rằng phương trình luôn có hai nghiệm phân biệt với mọi giá trị của \(b\).
b) Tìm \(b\) để phương trình có hai nghiệm \({x_1},{x_2}\) sao cho \({x_1} + {x_2} =  - 5\).
Câu 14: (1,50 điểm) Giải các phương trình và hệ phương trình sau:
a) \(\left( {x - 2} \right)\left( {2x + 1} \right) = 0\);

b) \(\frac{{x - 1}}{{x + 1}} + \frac{5}{{3x}} = 1\);

c) \(\left\{ {\begin{array}{*{20}{l}}{2x + y = 1}\\{x + 2y =  - 4}\end{array}} \right.\).
Câu 15: (2,00 điểm) Giải bài toán bằng cách lập phương trình.
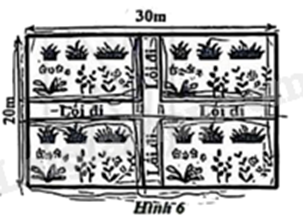
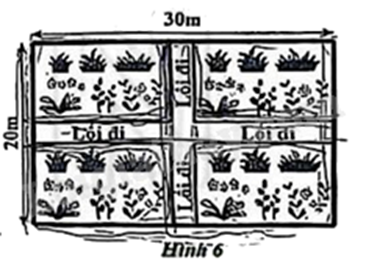
Để xây dựng công viên từ một mảnh đất hình chữ nhật có chiều dài 30 m, chiều rộng 20 m; người ta làm hai lối đi có bề rộng như nhau (hai lối đi này lần lượt song song với chiều dài và chiều rộng của mảnh đất), phần đất còn lại để trồng hoa (Hình 6). Xác định bề rộng của lối đi để phần đất trồng hoa có diện tích là 504 \({m^2}\).

Câu 16: (2,00 điểm) Cho hình chữ nhật \(ABCD\) có \(AB > AD\). Trên tia đối của tia \(BC\) lấy điểm \(E\) (\(E \ne B\)). Đường thẳng qua \(D\) và vuông góc với \(DE\) cắt đường thẳng \(AB\) tại \(F\). Gọi \(H\) là hình chiếu vuông góc của điểm \(D\) trên đường thẳng \(EF\).
a) Chứng minh bốn điểm \(D,F,B,E\) cùng thuộc một đường tròn.
b) Gọi \(I\) là giao điểm của \(ED\) và \(BF\); \(K\) là giao điểm của \(HD\) và \(BF\). Chứng minh \(FK.FB = FA.FI\).
c) Chứng minh rằng khi điểm \(E\) di chuyển trên tia đối của tia \(BC\) thì điểm \(H\) luôn chạy trên một đường cố định.

----------HẾT----------

Lời giải

I. TRẮC NGHIỆM:

Câu 1: Biểu thức nào sau đây có giá trị khác với các biểu thức còn lại?

A. \(\sqrt 9 \).

B. \({( - \sqrt 3 )^2}\).

C. \(\sqrt {{{( - 3)}^2}} \).

D. \( - {(\sqrt 3 )^2}\).

Phương pháp:

Sử dụng tính chất của căn bậc hai để xác định.

Lời giải:

Ta có:

\(\sqrt 9  = 3\)

\({( - \sqrt 3 )^2} = 3\)

\(\sqrt {{{( - 3)}^2}}  = \sqrt 9  = 3\)

\( - {(\sqrt 3 )^2} =  - 3\)

Vậy \( - {(\sqrt 3 )^2}\) có giá trị khác với các biểu thức còn lại.

Đáp án: D

Câu 2: Cho bất đẳng thức \(a > b\). Kết luận nào sau đây là không đúng?

A. \(3a > 3b\).

B. \(a - 1 < b - 1\).

C. \(a + 1 > b + 1\).

D. \( - 3a <  - 3b\).

Phương pháp:

Sử dụng tính chất của bất đẳng thức với phép cộng, phép nhân.

Lời giải:

Vì \(a > b\) và \(3 > 0\) nên \(3a > 3b\).

Vì \(a > b\) nên \(a - 1 > b - 1\) nên B sai.

Vì \(a > b\) nên \(a + 1 > b + 1\).

Vì \(a > b\) và \( - 3 < 0\) nên \( - 3a <  - 3b\).

Đáp án: B

Câu 3: Số nào sau đây không phải là một nghiệm của bất phương trình \(5x - 6 < 0\)?

A. \(\frac{5}{6}\).

B. \( - \frac{5}{6}\).

C. \(\frac{6}{5}\).

D. \( - \frac{6}{5}\).

Phương pháp:

Giải để tìm nghiệm của bất phương trình.

So sánh các đáp án với nghiệm của bất phương trình.

Lời giải:

Ta có: \(5x - 6 < 0\)

            \(5x < 6\)

              \(x < \frac{6}{5}\)

Trong các số trên, số \(\frac{6}{5}\) không thoả mãn \(x < \frac{6}{5}\).

Vậy \(\frac{6}{5}\) không phải là một nghiệm của bất phương trình.

Đáp án: C

Câu 4: Cặp số \(\left( {x;y} \right)\) nào sau đây là nghiệm của hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{3x - y = 1}\\{ - x + y = 1}\end{array}} \right.\)?

A. \(\left( {1;2} \right)\).

B. \(\left( {0; - 1} \right)\).

C. \(\left( {0;1} \right)\).

D. \(\left( {2;1} \right)\).

Phương pháp:

Đối với bài tập trắc nghiệm, ta sử dụng máy tính cầm tay để tính nghiệm.

Lời giải:

Sử dụng máy tính cầm tay, ta được \(\left( {x;y} \right) = \left( {1;2} \right)\).

Đáp án: A

Câu 5: Giả sử đồ thị của hàm số \(y = a{x^2}\) là parabol như Hình 1. Giá trị của \({x_0}\) bằng

A. \(2\).

B. \(\sqrt 3 \).

C. \( - 1,5\).

D. \( - \sqrt 2 \).

Phương pháp:

Dựa vào đồ thị ta thấy điểm A(1;2) thuộc đồ thị hàm số \(y = a{x^2}\) nên ta xác định được hàm số.

Xác định tung độ tương ứng với hoành độ \({x_0}\).

Thay vào hàm số để tìm \({x_0}\).

Lời giải:

Vì đồ thị của hàm số \(y = a{x^2}\) đi qua điểm \(A\left( {1;2} \right)\) nên ta có: \(2 = a{.1^2}\), suy ra \(a = 2\).

Do đó đồ thị này của hàm số \(y = 2{x^2}\).

Vì giá trị của \(y\) tại \({x_0}\) là \(4\) nên ta có: \(4 = 2.x_0^2\), suy ra \(x_0^2 = \frac{4}{2} = 2\), suy ra \({x_0} =  - \sqrt 2 \) (do \({x_0} < 0\)).

Đáp án: D

Câu 6: Tam giác \(ABC\) vuông tại \(A\) có đường cao \(AH\) (Hình 2). Khẳng định nào sau đây sai?

A. \({\rm{sin}}\alpha  = \frac{{AC}}{{BC}}\).

B. \({\rm{cos}}\alpha  = \frac{{BH}}{{BA}}\).

C. \({\rm{tan}}\beta  = \frac{{AB}}{{AC}}\).

D. \({\rm{cot}}\beta  = \frac{{AC}}{{AH}}\).

Phương pháp:

Dựa vào kiến thức về tỉ số lượng giác trong tam giác.

Lời giải:

Ta có:

\(\sin \alpha  = \frac{{AC}}{{BC}}\) nên A đúng.

\(\cos \alpha  = \frac{{BH}}{{BA}}\) nên B đúng.

\(\tan \beta  = \frac{{AB}}{{AC}}\) nên C đúng.

\(\cot \beta  = \frac{{HC}}{{AH}}\) nên D sai.

Đáp án: D

Câu 7: Tâm đường tròn nội tiếp tam giác là giao điểm của ba đường nào trong tam giác đó?

A. Đường phân giác.

B. Đường trung trực.

C. Đường cao.

D. Đường trung tuyến.

Phương pháp:

Sử dụng kiến thức về đường tròn nội tiếp tam giác.

Lời giải:

Tâm đường tròn nội tiếp tam giác là giao điểm của ba đường phân giác trong tam giác.

Đáp án: A

Câu 8: Một tam giác vuông có hai cạnh góc vuông lần lượt là \(5\) cm và \(12\) cm. Bán kính của đường tròn ngoại tiếp tam giác vuông đó bằng

A. \(8,5\) cm.

B. \(6,5\) cm.

C. \(13\) cm.

D. \(17\) cm.

Phương pháp:

Bán kính của đường tròn ngoại tiếp tam giác vuông bằng một nửa cạnh huyền.

Lời giải:

Cạnh huyền của tam giác vuông đó là: \(\sqrt {{5^2} + {{12}^2}}  = 13\) (cm)

Bán kính của đường tròn ngoại tiếp tam giác vuông đó là: 13 : 2 = 6,5 (cm)

Đáp án: B

Câu 9: Mỗi hình a), b), c), d) trên Hình 3 là hai đường tròn phân biệt \(\left( {O;R} \right)\) và \(\left( {O';R'} \right)\). Hình nào có đoạn nối tâm và hai bán kính thỏa mãn \(OO' > R + R'\)?

A. Hình 3a).

B. Hình 3b).

C. Hình 3c).

D. Hình 3d).

Phương pháp:

Dựa vào mối liên hệ giữa OO’ với R + R’.

Lời giải:

Vì \(OO' > R + R'\) nên hai đường tròn không giao nhau nên hình biểu diễn là hình 3c).

Đáp án: C

Câu 10: Cho tam giác \(ABC\) có \(\widehat {BAC} = 70^\circ \); \(\widehat {ABC} = 60^\circ \) nội tiếp đường tròn tâm \(O\) (Hình 4). Số đo của góc \(\widehat {AOB}\) bằng

A. \(50^\circ \).

B. \(100^\circ \).

C. \(120^\circ \).

D. \(140^\circ \).

Phương pháp:

Dựa vào định lí tổng ba góc trong tam giác bằng \(180^\circ \) suy ra \(\widehat {ACB}\).

Góc nội tiếp bằng một nửa góc ở tâm chắn cung đó.

Lời giải:

Áp dụng định lí tổng ba góc trong tam giác ABC, ta có:

\(\widehat {BAC} + \widehat {ABC} + \widehat {ACB} = 180^\circ \)

suy ra \(\widehat {ACB} = 180^\circ  - \widehat {BAC} - \widehat {ABC}\) \( = 180^\circ  - 70^\circ  - 60^\circ  = 50^\circ \)

Vì \(\widehat {ACB}\) và \(\widehat {AOB}\) lần lượt là góc nội tiếp và góc ở tâm chắn cung AB nên \(\widehat {AOB} = 2.\widehat {ACB} = 2.50^\circ  = 100^\circ \).

Đáp án: B

Câu 11: Thể tích của một hình trụ có đường kính đáy bằng 4 cm và chiều cao bằng 8 cm (Hình 5) là

A. \(64\pi c{m^3}\)

B. \(32\pi c{m^3}\)

C. \(\frac{{64\pi }}{3}c{m^3}\)

D. \(\frac{{32\pi }}{3}c{m^3}\)

Phương pháp:

Sử dụng công thức tính thể tích hình trụ: \(V = \pi {r^2}h\).

Lời giải:

Bán kính đáy của hình trụ là: \(4:2 = 2\left( {cm} \right)\)

Thể tích của hình trụ là: \(V = \pi {r^2}h = \pi {.2^2}.8 = 32\pi \left( {c{m^3}} \right)\).

Đáp án: B

Câu 12: Gieo đồng thời hai con xúc xắc cân đối, đồng chất. Xác suất của biến cố “tích của hai số chấm xuất hiện trên hai con xúc xắc bằng 7” là

A. 0

B. \(\frac{1}{{12}}\)

C. \(\frac{1}{7}\)

D. \(\frac{1}{6}\)

Phương pháp:

Xác định số phần tử của không gian mẫu.

Xác định số kết quả thuận lợi cho biến cố.

Xác suất của biến cố = số kết quả thuận lợi : số phần tử của không gian mẫu.

Lời giải:

Không gian mẫu của phép thử là:

\(\Omega  = \left\{ \begin{array}{l}\left( {1;1} \right),\left( {2;1} \right),\left( {3;1} \right),\left( {4;1} \right),\left( {5;1} \right),\left( {6;1} \right),\\\left( {1;2} \right),\left( {2;2} \right),\left( {3;2} \right),\left( {4;2} \right),\left( {5;2} \right),\left( {6;2} \right),\\\left( {1;3} \right),\left( {2;3} \right),\left( {3;3} \right),\left( {4;3} \right),\left( {5;3} \right),\left( {6;3} \right),\\\left( {1;4} \right),\left( {2;4} \right),\left( {3;4} \right),\left( {4;4} \right),\left( {5;4} \right),\left( {6;4} \right),\\\left( {1;5} \right),\left( {2;5} \right),\left( {3;5} \right),\left( {4;5} \right),\left( {5;5} \right),\left( {6;5} \right),\\\left( {1;6} \right),\left( {2;6} \right),\left( {3;6} \right),\left( {4;6} \right),\left( {5;6} \right),\left( {6;6} \right)\end{array} \right\}\)

Không gian mẫu có 36 phần tử.

Không có kết quả nào thuận lợi cho biến cố “tích của hai số chấm xuất hiện trên hai con xúc xắc bằng 7”.

Do đó xác suất của biến cố A là 0.

Đáp án: A

II. TỰ LUẬN: 

Câu 13: (1,50 điểm)
1) Rút gọn biểu thức \(A = \sqrt {{{(\sqrt 3  - 2)}^2}}  - \frac{3}{{\sqrt 3 }} + \sqrt {12} \).
2) Cho phương trình bậc hai (ẩn \(x\)): \(2{x^2} + bx - 3 = 0\).
a) Chứng tỏ rằng phương trình luôn có hai nghiệm phân biệt với mọi giá trị của \(b\).
b) Tìm \(b\) để phương trình có hai nghiệm \({x_1},{x_2}\) sao cho \({x_1} + {x_2} =  - 5\).
Phương pháp:

1) Khi rút gọn biểu thức, ta cần thực hiện theo các bước sau:

+ Bước 1: Tìm điều kiện xác định (nếu cần);

+ Bước 2: Phân tích mẫu thành nhân tử để tìm mẫu thức chung rồi quy đồng;

+ Bước 3: Áp dụng các phép toán (cộng, trừ, nhân, chia) phân thức kết hoặc các phép biến đổi khai căn để rút gọn phân thức.

2)

a) Chứng minh \(\Delta  > 0\) với mọi giá trị của b.

b) Áp dụng định lí Viète, ta có: \({x_1} + {x_2}\).

Thay vào \({x_1} + {x_2} =  - 5\) để tìm b.

Lời giải:

1) \(A = \sqrt {{{\left( {\sqrt 3  - 2} \right)}^2}}  - \frac{3}{{\sqrt 3 }} + \sqrt {12} \)

\( = \left| {\sqrt 3  - 2} \right| - \sqrt 3  + \sqrt {4.3} \)

\( = 2 - \sqrt 3  - \sqrt 3  + 2\sqrt 3 \)

\( = 2\).

Vậy \(A = 2\).

2)

a) Ta có \(\Delta  = {b^2} - 4.2.( - 3) = {b^2} + 24 > 0\) với mọi \(b\) nên phương trình luôn có hai nghiệm phân biệt với mọi giá trị của \(b\).

b) Áp dụng định lí Viète, ta có: \({x_1} + {x_2} =  - \frac{b}{2}\).

Để \({x_1} + {x_2} =  - 5\) thì \( - \frac{b}{2} =  - 5\), suy ra \(b = 10\).

Câu 14: (1,50 điểm) Giải các phương trình và hệ phương trình sau:
a) \(\left( {x - 2} \right)\left( {2x + 1} \right) = 0\);
b) \(\frac{{x - 1}}{{x + 1}} + \frac{5}{{3x}} = 1\);
c) \(\left\{ {\begin{array}{*{20}{l}}{2x + y = 1}\\{x + 2y =  - 4}\end{array}} \right.\).
Phương pháp:

a) Giải phương trình tích: \(\left( {ax + b} \right)\left( {cx + d} \right) = 0\) thì \(ax + b = 0\) hoặc \(cx + d = 0\).

b) Tìm điều kiện xác định, đưa phương trình chứa ẩn ở mẫu về phương trình bậc nhất một ẩn để giải.

c) Giải hệ phương trình bằng phương pháp cộng đại số.

Lời giải:

a) Để giải phương trình trên ta giải hai phương trình sau:

+) \(x - 2 = 0\) suy ra \(x = 2\)

+) \(2x + 1 = 0\) suy ra \(x =  - \frac{1}{2}\)

Vậy phương trình có nghiệm \(x = 2\) và \(x =  - \frac{1}{2}\)

b) ĐK: \(x \ne 0;\,\,x \ne  - 1\)

\(\frac{{x - 1}}{{x + 1}} + \frac{5}{{3x}} = 1\)

\(\frac{{3x(x - 1)}}{{3x(x + 1)}} + \frac{{5(x + 1)}}{{3x(x + 1)}} = \frac{{3x(x + 1)}}{{3x(x + 1)}}\)

\(3{x^2} - 3x + 5x + 5 = 3{x^2} + 3x\)

\( - x =  - 5\)

\(x = 5\) (tmđk)

Vậy nghiệm của phương trình là \(x = 5\).

c) \(\left\{ {\begin{array}{*{20}{l}}{2x + y = 1}\\{x + 2y =  - 4}\end{array}} \right.\)

\(\left\{ {\begin{array}{*{20}{l}}{4x + 2y = 2}\\{x + 2y =  - 4}\end{array}} \right.\)

\(\left\{ {\begin{array}{*{20}{l}}{3x = 6}\\{x + 2y =  - 4}\end{array}} \right.\)

\(\left\{ {\begin{array}{*{20}{l}}{x = 2}\\{y =  - 3}\end{array}} \right.\)

Vậy nghiệm của hệ phương trình là \((x;y) = (2; - 3)\)

Câu 15: (2,00 điểm) Giải bài toán bằng cách lập phương trình.
Để xây dựng công viên từ một mảnh đất hình chữ nhật có chiều dài 30 m, chiều rộng 20 m; người ta làm hai lối đi có bề rộng như nhau (hai lối đi này lần lượt song song với chiều dài và chiều rộng của mảnh đất), phần đất còn lại để trồng hoa (Hình 6). Xác định bề rộng của lối đi để phần đất trồng hoa có diện tích là 504 \({m^2}\).

Phương pháp:

Gọi bề rộng của lối đi là \(x\left( m \right)\), \(0 < x < \frac{{20}}{2} = 10\).

Tính diện tích của một phần đất trồng hoa.

Biểu diễn chiều dài của một phần đất trồng hoa sau khi làm lối đi, chiều rộng của một phần đất trồng hoa sau khi làm lối đi theo \(x\) suy ra diện tích của một phần đất trồng hoa sau khi làm lối đi.

Vì diện tích một phần đất trồng hoa là \(126{m^2}\) nên ta lập được phương trình.

Giải phương trình để tìm \(x\).

Kiểm tra điều kiện và kết luận.

Lời giải:

Gọi bề rộng của lối đi là \(x\left( m \right)\), \(0 < x < \frac{{20}}{2} = 10\).

Diện tích của một phần đất trồng hoa là: \(504:4 = 126\,\,({m^2})\)

Chiều dài của một phần đất trồng hoa sau khi làm lối đi là \(\frac{{30 - x}}{2}\left( m \right)\), chiều rộng của một phần đất trồng hoa sau khi làm lối đi là \(\frac{{20 - x}}{2}\left( m \right)\).

Diện tích của một phần đất trồng hoa sau khi làm lối đi là: \(\frac{{\left( {30 - x} \right)\left( {20 - x} \right)}}{4}\left( {{m^2}} \right)\).

Vì diện tích một phần đất trồng hoa là \(126{m^2}\) nên ta có phương trình:

\(\begin{array}{l}\frac{{\left( {30 - x} \right)\left( {20 - x} \right)}}{4} = 126\\\left( {30 - x} \right)\left( {20 - x} \right) = 504\\600 - 30x - 20x + {x^2} - 504 = 0\\{x^2} - 50x + 96 = 0\end{array}\)

Giải phương trình, ta được: \({x_1} = 48\) (loại do \(0 < x < 10\)); \({x_2} = 2\) (thoả mãn)

Vậy bề rộng của lối đi là 2m.

Câu 16: (2,00 điểm) Cho hình chữ nhật \(ABCD\) có \(AB > AD\). Trên tia đối của tia \(BC\) lấy điểm \(E\) (\(E \ne B\)). Đường thẳng qua \(D\) và vuông góc với \(DE\) cắt đường thẳng \(AB\) tại \(F\). Gọi \(H\) là hình chiếu vuông góc của điểm \(D\) trên đường thẳng \(EF\).
a) Chứng minh bốn điểm \(D,F,B,E\) cùng thuộc một đường tròn.
b) Gọi \(I\) là giao điểm của \(ED\) và \(BF\); \(K\) là giao điểm của \(HD\) và \(BF\). Chứng minh \(FK.FB = FA.FI\).
c) Chứng minh rằng khi điểm \(E\) di chuyển trên tia đối của tia \(BC\) thì điểm \(H\) luôn chạy trên một đường cố định.

Phương pháp:

a) Chứng minh \(\Delta EDF\) vuông tại D, \(\Delta BEF\) vuông tại B nên E, F, B, D cùng thuộc đường tròn đường kính EF.

b) Chứng minh $\Delta FKH\backsim \Delta FEB\left( g.g \right)$ nên $FK.FB=FE.FH$

Chứng minh $\Delta FHD\backsim \Delta FDE\left( g.g \right)$ nên $F{{D}^{2}}=FH.FE$

Chứng minh $\Delta FAD\backsim \Delta FDI\left( g.g \right)$ nên \(F{D^2} = FA.FI\)

Suy ra \(FK.FB = FA.FI\)

c) Chứng minh tứ giác AHFD nội tiếp đường tròn đường kính FD.

Suy ra \(\angle FAH = \angle FDH\). Từ đó suy ra \(\angle FAH = \angle BAC\)

Kết hợp với \(\angle HAB + \angle FAH = 180^\circ \) suy ra \(\angle HAB + \angle BAC = 180^\circ \)

hay H, A, C thẳng hàng.

Kết luận điểm H luôn chạy trên một đường cố định AC.

Lời giải:

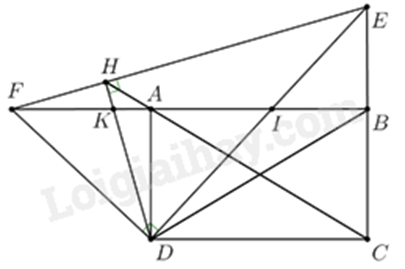
a) Do \(ED \bot FD\) nên \(\Delta EDF\) vuông tại D. Khi đó E, F, D cùng thuộc đường tròn đường kính EF

Có \(\Delta BEF\) vuông tại B (ABCD là hình chữ nhật) nên B, E, F  cùng thuộc đường tròn đường kính EF

Vậy E, F, B, D cùng thuộc đường tròn đường kính EF.

b) Xét \(\Delta FKH\) và \(\Delta FEB\) có \(\angle EFB\) chung và \(\angle FHK = \angle FBE\left( { = 90^\circ } \right)\)

Suy ra $\Delta FKH\backsim \Delta FEB\left( g.g \right)$ nên $\frac{FK}{FE}=\frac{FH}{FB}$ hay $FK.FB=FE.FH$  (1)

Tương tự $\Delta FHD\backsim \Delta FDE\left( g.g \right)$ ($\angle DFE$ chung và $\angle FHD=\angle FDE=90{}^\circ $) nên $F{{D}^{2}}=FH.FE$  (2)

$\Delta FAD\backsim \Delta FDI\left( g.g \right)$ ($\angle DFI$ chung và \(\angle FAD = \angle FDI = 90^\circ \)) nên \(F{D^2} = FA.FI\)   (3)

Từ (1), (2), (3) suy ra \(FK.FB = FA.FI\)

c) Ta có \(\angle FHD = \angle FAD = 90^\circ \)

Do đó A, H, F, D thuộc đường tròn đường kính FD hay tứ giác AHFD nội tiếp đường tròn đường kính FD.

Suy ra \(\angle FAH = \angle FDH\)

Mà \(\angle FDH = \angle FED = \angle FBD = \angle BAC\), \(\angle HAB + \angle FAH = 180^\circ \)

Nên \(\angle HAB + \angle BAC = 180^\circ \)

Hay H, A, C thẳng hàng.

Vậy khi điểm E di chuyển trên tia đối của tia BC thì điểm H luôn chạy trên một đường cố định A