Đề thi vào 10 môn Toán Kon Tum năm 2025

Đề bài

Câu 1: (2,5 điểm)

1) Thực hiện phép tính \(\sqrt 4  + 3\).

2) Giải bất phương trình \(x - 6 > 0\).

3) Cho hàm số \(y = {x^2}\). Tính giá trị của \(y\) khi \(x = 1\).

Câu 2: (2,5 điểm)

1) Sau khi thống kê độ dài (đơn vị: centimét) của 60 lá dương xỉ trưởng thành, người ta có bảng tần số ghép nhóm như sau:

Tìm tần số và tần số tương đối ghép nhóm của nhóm [20;30).

2) Một hộp có 10 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5, 6, 7, 8, 9, 10; hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp. Tính xác suất của biến cố A: “Số xuất hiện trên thẻ được rút ra là số nhỏ hơn 4”.

3) Lớp 9A được chia làm 2 tổ để hoàn thành 500 cái thiệp Tết trong một thời gian quy định. Nhờ tăng năng suất làm việc, tổ một vượt mức 10% và tổ hai vượt mức 20% nên cả hai tổ đã làm được 580 cái thiệp. Tính số thiệp làm theo kế hoạch của mỗi tổ.

Câu 3: (1,75 điểm)

1) Một chiếc mũ sinh nhật dạng hình nón (hình vẽ minh hoạ bên), biết chiều cao \(h = 24\;{\rm{cm}}\), bán kính đáy \(R = 10\;{\rm{cm}}\). Hỏi diện tích xung quanh của chiếc mũ sinh nhật đó là bao nhiêu centimét vuông (đây \(\pi  = 3,14\) và kết quả được làm tròn đến hàng phần mười)?

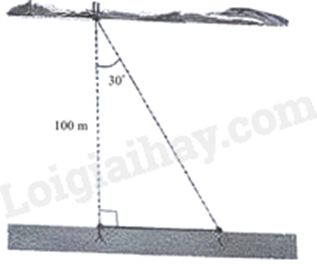
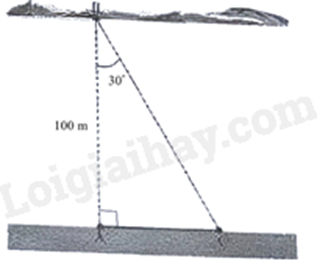
2) Hình vẽ bên minh họa một phần con sông có bề rộng \(AB = 100\;{\rm{m}}\). Một chiếc thuyền đi thẳng từ vị trí B bên này bờ sông đến vị trí C bên kia bờ sông. Hỏi khoảng cách BC bằng bao nhiêu mét (kết quả được làm tròn đến hàng phần mười), biết \(AB \bot AC\) và \(\angle ABC = 30^\circ \)?

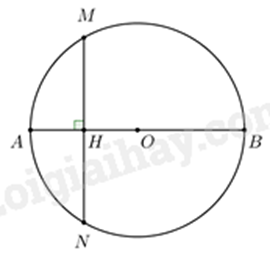
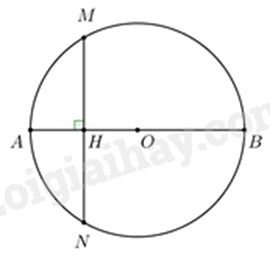
Câu 4: (2,5 điểm) Cho đường tròn tâm O, đường kính AB. Gọi H là trung điểm của đoạn thẳng AO, dây cung MA vuông góc với AO tại H. (Học sinh có thể tham khảo hình vẽ dưới đây và phải vẽ hình vào bài làm).

1) Chứng minh \(MA = MO\) và \(\Delta AMO\) đều.

2) Trên tia OA lấy điểm C sao cho A là trung điểm của đoạn thẳng OC. Qua C vẽ đường thẳng cắt đoạn thẳng MH tại K (K khác hai điểm M và H), cắt đường tròn đã cho tại hai điểm E, F (E nằm giữa C và F). Gọi I là trung điểm của đoạn thẳng EF.

Chứng minh tứ giác CMIO nội tiếp và \(C{M^2} = CI \cdot CK\).

Câu 5: (1,5 điểm)

1) Rút gọn biểu thức \(A = \left( {\frac{{ - 2}}{{x - 1}} + \frac{1}{{\sqrt x  - 1}}} \right):\frac{{2\sqrt x }}{{x + \sqrt x }}\), với \(x > 0\) và \(x \ne 1\).

2) Cho phương trình \({x^2} - 7x + 5 = 0\), biết phương trình có hai nghiệm là \({x_1},{x_2}\). Không giải phương trình, tính giá trị của biểu thức \(P = \left| {{x_2} - 3} \right| + \sqrt {{x_1} + 4} \).

----- HẾT -----

Lời giải

Câu 1: (2,5 điểm)

1) Thực hiện phép tính \(\sqrt 4  + 3\).

2) Giải bất phương trình \(x - 6 > 0\).

3) Cho hàm số \(y = {x^2}\). Tính giá trị của \(y\) khi \(x = 1\).

Phương pháp:

1) Tính căn bậc hai sau đó thực hiện phép cộng.

2) Chuyển vế để giải bất phương trình bậc nhất một ẩn.

3) Thay \(x = 1\) vào hàm số để tìm \(y\).

Lời giải:

1) \(\sqrt 4  + 3 = 2 + 3 = 5\).

2) \(x - 6 > 0\)

\(x > 6\).

Vậy bất phương trình có nghiệm là \(x > 6\).

3) Thay \(x = 1\) vào hàm số \(y = {x^2}\), ta được:

\(y = {1^2} = 1\).

Vậy khi \(x = 1\) thì \(y = 1\).

Câu 2: (2,5 điểm)

1) Sau khi thống kê độ dài (đơn vị: centimét) của 60 lá dương xỉ trưởng thành, người ta có bảng tần số ghép nhóm như sau:

Tìm tần số và tần số tương đối ghép nhóm của nhóm [20;30).

2) Một hộp có 10 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5, 6, 7, 8, 9, 10; hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp. Tính xác suất của biến cố A: “Số xuất hiện trên thẻ được rút ra là số nhỏ hơn 4”.

3) Lớp 9A được chia làm 2 tổ để hoàn thành 500 cái thiệp Tết trong một thời gian quy định. Nhờ tăng năng suất làm việc, tổ một vượt mức 10% và tổ hai vượt mức 20% nên cả hai tổ đã làm được 580 cái thiệp. Tính số thiệp làm theo kế hoạch của mỗi tổ.

Phương pháp:

1) Quan sát bảng tần số ghép nhóm để tìm tần số của nhóm [20;30).

Tần số tương đối ghép nhóm tính bằng công thức: \({f_x} = \frac{m}{N}.100\% \) (m là tần số của nhóm \(x\), N là cỡ mẫu).

2) Xác định số kết quả có thể, số kết quả thuận lợi cho biến cố.

Xác suất của biến cố = số kết quả thuận lợi : số kết quả có thể.

3) Gọi số thiệp tổ một và tổ hai làm theo kế hoạch lần lượt là \(x\) và \(y\) (cái), \(x,y \in {\mathbb{N}^*},0 < x,y < 500\).

Vì theo kế hoạch hai tổ cần làm 500 cái thiệp nên ta lập được phương trình thứ nhất.

Vì thực tế tổ một làm vượt mức 10%, tổ hai làm vượt mức 20% và hai tổ làm được 580 cái thiệp nên ta lập được phương trình thứ hai.

Từ (1) và (2) ta có hệ phương trình.

Giải hệ phương trình.

Kiểm tra điều kiện và kết luận.

Lời giải:

1) Tần số ghép nhóm của nhóm [20;30) là 15.

Tần số tương đối ghép nhóm của nhóm [20;30) là: \(\frac{{15}}{{60}}.100\%  = 25\% \).

2) Số kết quả có thể khi rút ngẫu nhiên một thẻ trong hộp là 10, đó là: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.

Số kết quả thuận lợi cho biến cố A: “Số xuất hiện trên thẻ được rút ra là số nhỏ hơn 4” là 3, đó là: 1, 2, 3.

Vậy xác suất của biến cố A: “Số xuất hiện trên thẻ được rút ra là số nhỏ hơn 4” là: \(\frac{3}{{10}}\)

3) Gọi số thiệp tổ một và tổ hai làm theo kế hoạch lần lượt là \(x\) và \(y\) (cái), \(x,y \in {\mathbb{N}^*},0 < x,y < 500\).

Vì theo kế hoạch hai tổ cần làm 500 cái thiệp nên ta có phương trình: \(x + y = 500\) (1)

Thực tế, tổ một làm vượt mức 10% nên số thiệp tổ một làm được là: \(x + 10\% x = 1,1x\) (cái)

              tổ hai làm vượt mức 20% nên số thiệp tổ hai làm được là: \(y + 20\% y = 1,2y\) (cái)

Vì thực tế hai tổ làm được 580 cái thiệp nên ta có phương trình: \(1,1x + 1,2y = 580\) (2)

Từ (1) và (2) ta có hệ phương trình: \(\left\{ \begin{array}{l}x + y = 500\\1,1x + 1,2y = 580\end{array} \right.\).

Giải hệ phương trình, ta được: \(\left\{ \begin{array}{l}x = 200\\y = 300\end{array} \right.\) (TM)

Vậy theo kế hoạch tổ một và tổ hai làm được lần lượt 200 cái thiệp và 300 cái thiệp.

Câu 3: (1,75 điểm)

1) Một chiếc mũ sinh nhật dạng hình nón (hình vẽ minh hoạ bên), biết chiều cao \(h = 24\;{\rm{cm}}\), bán kính đáy \(R = 10\;{\rm{cm}}\). Hỏi diện tích xung quanh của chiếc mũ sinh nhật đó là bao nhiêu centimét vuông (đây \(\pi  = 3,14\) và kết quả được làm tròn đến hàng phần mười)?

2) Hình vẽ bên minh họa một phần con sông có bề rộng \(AB = 100\;{\rm{m}}\). Một chiếc thuyền đi thẳng từ vị trí B bên này bờ sông đến vị trí C bên kia bờ sông. Hỏi khoảng cách BC bằng bao nhiêu mét (kết quả được làm tròn đến hàng phần mười), biết \(AB \bot AC\) và \(\angle ABC = 30^\circ \)?

Phương pháp:

1) Sử dụng định lí Pythagore để tính đường sinh của chiếc mũ hình nón.

Diện tích xung quanh của chiếc mũ hình nón: \(S = \pi rl\).

2) Áp dụng tỉ số lượng giác của góc nhọn trong tam giác vuông, ta biểu diễn tỉ số lượng giác liên quan đến \(\angle ABC\), AB và BC. Từ đó tính BC.

Lời giải:

1) Đường sinh của chiếc mũ hình nón là \(l = \sqrt {{R^2} + {h^2}}  = \sqrt {{{10}^2} + {{24}^2}}  = 26\)cm.

Diện tích xung quanh của chiếc mũ hình nón là \(S = \pi Rl = 3,14.10.26 = 816,4{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^2}} \right)\)

2) Xét tam giác ABC vuông tại A, ta có \(\cos \angle ABC = \frac{{AB}}{{BC}}\)

Suy ra \(BC = \frac{{AB}}{{\cos \angle ABC}} = \frac{{100}}{{\cos 30^\circ }} \approx 115,5\)m

Vậy khoảng cách BC là 115,5m.

Câu 4: (2,5 điểm) Cho đường tròn tâm O, đường kính AB. Gọi H là trung điểm của đoạn thẳng AO, dây cung MA vuông góc với AO tại H. (Học sinh có thể tham khảo hình vẽ dưới đây và phải vẽ hình vào bài làm).

1) Chứng minh \(MA = MO\) và \(\Delta AMO\) đều.

2) Trên tia OA lấy điểm C sao cho A là trung điểm của đoạn thẳng OC. Qua C vẽ đường thẳng cắt đoạn thẳng MH tại K (K khác hai điểm M và H), cắt đường tròn đã cho tại hai điểm E, F (E nằm giữa C và F). Gọi I là trung điểm của đoạn thẳng EF.

Chứng minh tứ giác CMIO nội tiếp và \(C{M^2} = CI \cdot CK\).

Phương pháp:

1) Chứng minh tam giác AMO cân tại M nên MA = MO.

Chứng minh MA = MO = AO nên tam giác AMO đều.

2) * Chứng minh \(\Delta COM\) vuông tại M, \(\Delta OIC\) vuông tại I nên O, I, M, C thuộc đường tròn đường kính OC hay tứ giác CMIO nội tiếp.

* Chứng minh $\Delta CHK\backsim \Delta CIO\left( g.g \right)$ suy ra $CH.CO=CI.CK$

Chứng minh $\Delta CMH\backsim \Delta COM\left( g.g \right)$ suy ra \(C{M^2} = CH.CO\)

Do đó \(C{M^2} = CK.CI\)

Lời giải:

1)

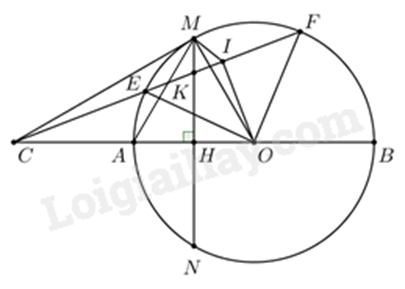
Xét \(\Delta MAO\) có MH vừa là đường cao vừa là trung tuyến nên \(\Delta MAO\) cân tại M

Suy ra \(MA = MO\) (tính chất tam giác cân)

Do \(OM = OA\) (cùng bằng bán kính của \(\left( O \right)\)) mà \(MA = MO\) nên \(OM = OA = MA\)

Suy ra \(\Delta OMA\) đều

2) Do A là trung điểm của OC nên \(AC = AO\)

Mà \(AO = AM\) (do \(\Delta OMA\) đều) nên \(AO = AC = AM\)

nên \(\Delta COM\) vuông tại M, suy ra C, O, M thuộc đường tròn đường kính OC

Lại có \(\Delta OEF\) cân tại O (do \(OE = OF\) là bán kính của \(\left( O \right)\)) có OI là trung tuyến nên OI đồng thời là đường cao. Suy ra \(\Delta OIC\) vuông tại I nên O, I, C thuộc đường tròn đường kính OC

Vậy O, I, M, C thuộc đường tròn đường kính OC hay tứ giác CMIO nội tiếp

Xét \(\Delta CHK\) và \(\Delta CIO\) có \(\angle OCI\) chung và \(\angle CHK = \angle CIO\left( { = 90^\circ } \right)\)

Nên $\Delta CHK\backsim \Delta CIO\left( g.g \right)$. Khi đó $\frac{CH}{CI}=\frac{CK}{CO}$ hay $CH.CO=CI.CK$ (1)

Tương tự $\Delta CMH\backsim \Delta COM$ (do \(\angle OCM\) chung và \(\angle CHM = \angle CMO = 90^\circ \))

Nên \(\frac{{CM}}{{CO}} = \frac{{CH}}{{CM}}\) hay \(C{M^2} = CH.CO\)  (2)

Từ (1) và (2) suy ra \(C{M^2} = CK.CI\)

Câu 5: (1,5 điểm)

1) Rút gọn biểu thức \(A = \left( {\frac{{ - 2}}{{x - 1}} + \frac{1}{{\sqrt x  - 1}}} \right):\frac{{2\sqrt x }}{{x + \sqrt x }}\), với \(x > 0\) và \(x \ne 1\).

2) Cho phương trình \({x^2} - 7x + 5 = 0\), biết phương trình có hai nghiệm là \({x_1},{x_2}\). Không giải phương trình, tính giá trị của biểu thức \(P = \left| {{x_2} - 3} \right| + \sqrt {{x_1} + 4} \).

Phương pháp:

1) Sử dụng tính chất của căn thức bậc hai để rút gọn biểu thức chứa căn.

2) Chứng minh phương trình có hai nghiệm phân biệt.

Áp dụng định lí Viète để có \({x_1} + {x_2};{x_1}{x_2}\).

Chứng minh \(\sqrt {{x_1} + 4}  = \left| {{x_1} - 3} \right|\) bằng cách thay \({x_1}\) vào \({x^2} - 7x + 5 = 0\).

Biển đổi P để xuất hiện tổng và tích của hai nghiệm.

Lời giải:

1) ĐK: \(x > 0\) và \(x \ne 1\)

\(A = \left( {\frac{{ - 2}}{{x - 1}} + \frac{1}{{\sqrt x  - 1}}} \right):\frac{{2\sqrt x }}{{x + \sqrt x }}\)

\(A = \left( {\frac{{ - 2}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}} + \frac{{\sqrt x  + 1}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}} \right):\frac{{2\sqrt x }}{{\sqrt x \left( {\sqrt x  + 1} \right)}}\)

\(A = \frac{{ - 2 + \sqrt x  + 1}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}:\frac{2}{{\sqrt x  + 1}}\)

\(A = \frac{{\sqrt x  - 1}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}.\frac{{\sqrt x  + 1}}{2}\)

\(A = \frac{1}{2}\)

Vậy \(A = \frac{1}{2}\) với \(x > 0\) và \(x \ne 1\)

2) Do \({x_1},{x_2}\) là hai nghiệm của phương trình \({x^2} - 7x + 5 = 0\) nên áp dụng định lý Viete ta có \(\left\{ \begin{array}{l}{x_1} + {x_2} = 7\\{x_1}{x_2} = 5\end{array} \right.\)

Do \({x_1}\) là nghiệm của \({x^2} - 7x + 5 = 0\) nên \(x_1^2 - 7{x_1} + 5 = 0\) hay \({x_1} + 4 = x_1^2 - 6{x_1} + 9 = {\left( {{x_1} - 3} \right)^2}\)

Suy ra \(\sqrt {{x_1} + 4}  = \sqrt {{{\left( {{x_1} - 3} \right)}^2}}  = \left| {{x_1} - 3} \right|\)

Thay vào \(P = \left| {{x_2} - 3} \right| + \sqrt {{x_1} + 4} \) ta có \(P = \left| {{x_2} - 3} \right| + \left| {{x_1} - 3} \right|\)

Ta thấy \(P \ge 0\) nên

\(\begin{array}{l}{P^2} = {\left( {{x_1} - 3} \right)^2} + {\left( {{x_2} - 3} \right)^2} + 2\left| {\left( {{x_1} - 3} \right)\left( {{x_2} - 3} \right)} \right|\\\,\,\,\,\,\, = \left( {x_1^2 + x_2^2} \right) - 6\left( {{x_1} + {x_2}} \right) + 18 + 2\left| {{x_1}{x_2} - 3\left( {{x_1} + {x_2}} \right) + 9} \right|\\\,\,\,\,\,\, = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} - 6\left( {{x_1} + {x_2}} \right) + 18 + 2\left| {5 - 3.7 + 9} \right|\\\,\,\,\,\,\, = {7^2} - 4.5 - 6.7 + 18 + 2.7 = 29\end{array}\)

Vậy \(P = \sqrt {29} \)