Đề thi vào 10 môn Toán Bắc Kạn năm 2025

Đề bài

Câu 1: (1 điểm) a) Tính \(A = 5 + \sqrt 9 \); \(B = \sqrt {25}  - \sqrt 4 \).

b) Rút gọn biểu thức \(P = \left( {\frac{1}{{\sqrt x  - 3}} + \frac{1}{{\sqrt x  + 3}}} \right):\frac{{2\sqrt x }}{{x + 9}}\), với \(x > 0\), \(x \ne 9\).

Câu 2: (2 điểm) a) Giải phương trình\(x - 7 = 0\).

b) Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{x + 4y = 6}\\{3x - 4y = 2}\end{array}} \right.\).

c) Bình và An đi xe đạp điện từ A đến B , khời hành cùng một lúc. Biết vận tốc trung bình của An lớn hơn vận tốc trung bình của Bình là \(5\;{\rm{km}}/{\rm{h}}\), do đó An đến B trước Bình 6 phút. Biết quãng đường AB là 10km Tính vận tốc của mỗi xe.

Câu 3: (2 điểm) Thống kê điểm kiểm tra môn Toán cuối học kỳ II của 30 học sinh lớp 9A ở một trường THCS cho kết quả như sau:

a) Lập bảng tần số cho mẫu số liệu trên.

b) Tính xác suất của biến cố A: “Học sinh đạt điểm lớn hơn 7”.

Câu 4: (1,5 điểm) Cho Parabol (P): \(y = {x^2}\) và đường thẳng d: \(y = ax + b\).

a) Vẽ Parabol (P): \(y = {x^2}\) trên mặt phẳng toạ độ Oxy.

b) Tìm a, b để đường thẳng d đi qua điểm A(2;8) và song song với đường thẳng d’: \(y = 3x + 2025\).

c) Với a, b tìm được ở ý b) đường thẳng d cắt Parabol (P) tại hai điểm phân biệt có hoành độ lần lượt là \({x_1};{x_2}\). Hãy tính giá trị của biểu thức \(A = x_1^2 + x_2^2 - 5{x_1}{x_2}\).

Câu 5: (3,5 điểm) 1. Cho đường tròn (O) có bán kính bằng 3 cm. Từ điểm M nằm ngoài đường tròn (O) kẻ các tiếp tuyến MA, MB với (O) (A, B lần lượt là các tiếp điểm). Kẻ đường kính AC, tiếp tuyến tại C của (O) cắt AB tại D.

a) Chứng minh tứ giác OAMB nội tiếp.

b) Tính số đo của góc OCB, biết \(BC = 4\;{\rm{cm}}\).

c) Gọi N là giao điểm của MC và OD. Chứng minh \(\Delta MAC\) đồng dạng với \(\Delta CND\).

2. Một ly nước dạng hình nón có chiều cao 18cm, đường kính miệng ly 6cm. Lượng nước trong ly cao 12cm. Ly nước đặt cố định như hình vẽ (tức là hình nón đứng, đỉnh ở dưới). Tính thể tích phần nước trong ly.

Câu 6: (1 điểm) Trong một cuộc thi tuyển dụng việc làm, ban tổ chức quy định mỗi người ứng tuyển phải trả lời 30 câu hỏi ở vòng sơ tuyển. Mỗi câu hỏi này có sẵn bốn đáp án, trong đó chỉ có một đáp án đúng. Người ứng tuyển chọn đáp án đúng sẽ được cộng thêm 2 điểm, chọn đáp án sai bị trừ 1 điểm. Ở vòng sơ tuyển, ban tổ chức tặng cho mỗi người dự thi 6 điểm và theo quy định người ứng tuyển phải trả lời hết 30 câu hỏi, người nào có số điểm từ 27 trở lên mới được dự thi vòng tiếp theo. Hỏi người ứng tuyển phải trả lời đúng ít nhất bao nhiêu câu hỏi ở vòng sơ tuyển thì mới được vào vòng tiếp theo?

----HẾT----

Lời giải

Câu 1: (1 điểm) a) Tính \(A = 5 + \sqrt 9 \); \(B = \sqrt {25}  - \sqrt 4 \).

b) Rút gọn biểu thức \(P = \left( {\frac{1}{{\sqrt x  - 3}} + \frac{1}{{\sqrt x  + 3}}} \right):\frac{{2\sqrt x }}{{x + 9}}\), với \(x > 0\), \(x \ne 9\).

Phương pháp:

a) Sử dụng kiến thức \(\sqrt {{a^2}}  = \left| a \right|\).

b) Sử dụng kết hợp các kiến thức của căn thức bậc hai để rút gọn.

Lời giải:

a) \(A = 5 + \sqrt 9  = 5 + 3 = 8\)

\(B = \sqrt {25}  - \sqrt 4  = 5 - 2 = 3\)

b) \(P = \left( {\frac{1}{{\sqrt x  - 3}} + \frac{1}{{\sqrt x  + 3}}} \right):\frac{{2\sqrt x }}{{x + 9}}\) (với \(x > 0\), \(x \ne 9\))

\( = \left[ {\frac{{\sqrt x  + 3}}{{\left( {\sqrt x  + 3} \right)\left( {\sqrt x  - 3} \right)}} + \frac{{\sqrt x  - 3}}{{\left( {\sqrt x  + 3} \right)\left( {\sqrt x  - 3} \right)}}} \right]:\frac{{2\sqrt x }}{{x + 9}}\)

\( = \frac{{\sqrt x  + 3 + \sqrt x  - 3}}{{\left( {\sqrt x  + 3} \right)\left( {\sqrt x  - 3} \right)}}:\frac{{2\sqrt x }}{{x + 9}}\)

\( = \frac{{2\sqrt x }}{{\left( {\sqrt x  + 3} \right)\left( {\sqrt x  - 3} \right)}}.\frac{{x + 9}}{{2\sqrt x }}\)

\( = \frac{{x + 9}}{{x - 9}}\).

Vậy \(P = \frac{{x + 9}}{{x - 9}}\) với \(x > 0\), \(x \ne 9\).

Câu 2: (2 điểm) a) Giải phương trình \(x - 7 = 0\).

b) Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{x + 4y = 6}\\{3x - 4y = 2}\end{array}} \right.\).

c) Bình và An đi xe đạp điện từ A đến B, khời hành cùng một lúc. Biết vận tốc trung bình của An lớn hơn vận tốc trung bình của Bình là \(5\;{\rm{km}}/{\rm{h}}\), do đó An đến B trước Bình 6 phút. Biết quãng đường AB là 10km Tính vận tốc của mỗi xe.

Phương pháp:

a) Chuyển vế để giải phương trình bậc nhất một ẩn.

b) Sử dụng phương pháp cộng đại số để giải hệ phương trình bậc nhất hai ẩn.

c) Gọi \(x\left( {km/h} \right)\) là vận tốc trung bình của bạn Bình \(\left( {x > 0} \right)\)

Biểu diễn thời gian đi của Bình và An theo \(x\).

Do An đến B trước Bình 6 phút nên ta lập được phương trình.

Giải phương trình, kiểm tra nghiệm và kết luận.

Lời giải:

a) \(x - 7 = 0\)

\(x = 7\)

Vậy phương trình có nghiệm \(x = 7\).

b) \(\left\{ {\begin{array}{*{20}{l}}{x + 4y = 6}\\{3x - 4y = 2}\end{array}} \right.\)

\(\left\{ {\begin{array}{*{20}{l}}{x + 4y = 6}\\{4x = 8}\end{array}} \right.\)

\(\begin{array}{l}\left\{ {\begin{array}{*{20}{l}}{x + 4y = 6}\\{x = 2}\end{array}} \right.\\\left\{ {\begin{array}{*{20}{l}}{2 + 4y = 6}\\{x = 2}\end{array}} \right.\\\left\{ {\begin{array}{*{20}{l}}{4y = 4}\\{x = 2}\end{array}} \right.\\\left\{ {\begin{array}{*{20}{l}}{y = 1}\\{x = 2}\end{array}} \right.\end{array}\)

Vậy hệ phương trình có nghiệm \(\left( {x;y} \right) = \left( {2;1} \right)\).

c) Gọi \(x\left( {km/h} \right)\) là vận tốc trung bình của bạn Bình \(\left( {x > 0} \right)\)

Khi đó vận tốc trung bình của An là: \(x + 5\,\,\left( {km/h} \right)\)

Thời gian đi của Bình là: \(\frac{{10}}{x}\left( h \right)\)

Thời gian đi của An là: \(\frac{{10}}{{x + 5}}\left( h \right)\)

Do An đến B trước Bình 6 phút = \(\frac{1}{{10}}\left( h \right)\) nên ta có: \(\frac{{10}}{x} - \frac{{10}}{{x + 5}} = \frac{1}{{10}}\)

\(\frac{{10\left( {x + 5} \right)}}{{x\left( {x + 5} \right)}} - \frac{{10x}}{{x\left( {x + 5} \right)}} = \frac{1}{{10}}\)

\(\frac{{10x + 50 - 10x}}{{x\left( {x + 5} \right)}} = \frac{1}{{10}}\)

\(\frac{{50}}{{x\left( {x + 5} \right)}} = \frac{1}{{10}}\)

\(500 = x\left( {x + 5} \right)\)

\({x^2} + 5x - 500 = 0\)

Giải phương trình ta được \(x = 20\left( {tm} \right)\); \(x =  - 25\left( {ktm} \right)\)

Vậy vận tốc của Bình là 20km/h, vận tốc của An là 25km/h.

Câu 3: (2 điểm) Thống kê điểm kiểm tra môn Toán cuối học kỳ II của 30 học sinh lớp 9A ở một trường THCS cho kết quả như sau:

a) Lập bảng tần số cho mẫu số liệu trên.

b) Tính xác suất của biến cố A: “Học sinh đạt điểm lớn hơn 7”.

Phương pháp:

a) Dựa vào dãy dữ liệu để lập bảng tần số.

b) Xác định số phần tử của không gian mẫu.

Xác định số kết quả thuận lợi cho biến cố.

Xác suất của biến cố = số kết quả thuận lợi / số phần tử của không gian mẫu.

Lời giải:

a) Bảng tần số:

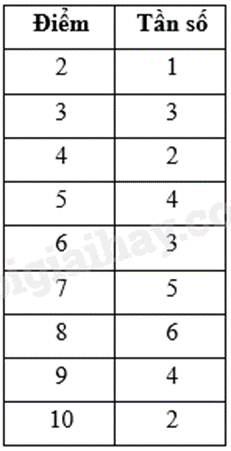
b) Số phần tử của không gian mẫu là \(n\left( \Omega  \right) = 30\).

Số học sinh đạt điểm lớn hơn 7 là: 6 + 4 + 2 = 12 (học sinh)

Do đó số phần tử của tập hợp A là \(n\left( A \right) = 12\).

Xác suất của biến cố A là: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega  \right)}} = \frac{{12}}{{30}} = 0,4\).

Câu 4: (1,5 điểm) Cho Parabol (P): \(y = {x^2}\) và đường thẳng d: \(y = ax + b\).

a) Vẽ Parabol (P): \(y = {x^2}\) trên mặt phẳng toạ độ Oxy.

b) Tìm a, b để đường thẳng d đi qua điểm A(2;8) và song song với đường thẳng d’: \(y = 3x + 2025\).

c) Với a, b tìm được ở ý b) đường thẳng d cắt Parabol (P) tại hai điểm phân biệt có hoành độ lần lượt là \({x_1};{x_2}\). Hãy tính giá trị của biểu thức \(A = x_1^2 + x_2^2 - 5{x_1}{x_2}\).

Phương pháp:

a) Lập bảng giá trị.

Xác định các điểm thuộc Parabol.

Vẽ đồ thị đi qua các điểm trên.

b) Đường thẳng d song song với đường thẳng d’: \(y = 3x + 2025\) nên ta xác định được hệ số a.

Đường thẳng d đi qua điểm A(2;8) nên ta thay toạ độ điểm A vào hàm số để tìm b.

c) Đường thẳng d: \(y = 3x + 2\) cắt Parabol (P): \(y = {x^2}\) nên ta có hoành độ bằng nhau.

Chứng minh phương trình có hai nghiệm phân biệt.

Sử dụng định lí Viète.

Biến đổi A, áp dụng định lí Viète để tính A.

Lời giải:

a) Ta có bảng giá trị sau:

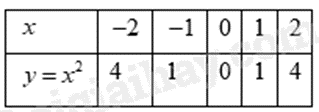
Đồ thị hàm số là đường cong parabol đi qua các điểm:

\(O\,\left( {0;0} \right);A\left( { - 2;4} \right);\,\,B\left( { - 1;1} \right);C\left( {1;1} \right);\,\,D\left( {2;4} \right)\)

Hệ số \(a = 1 > 0\)nên parabol có bề cong hướng lên. Đồ thị hàm số nhận Oy làm trục đối xứng.

Ta vẽ được đồ thị hàm số \(y = {x^2}\) như sau:

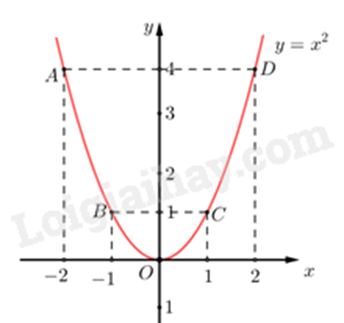
b) Vì đường thẳng d song song với đường thẳng d’ nên \(a = 3;b \ne 2025\), ta được đường thẳng d: \(y = 3x + b\).

Vì đường thẳng d đi qua điểm A(2;8) nên \(8 = 3.2 + b\), suy ra \(b = 8 - 3.2 = 2\) (tmđk). Đường thẳng d là: \(y = 3x + 2\).

Vậy \(a = 3;b = 2\).

c) Đường thẳng d: \(y = 3x + 2\) cắt Parabol (P): \(y = {x^2}\) thì ta có phương trình: \({x^2} = 3x + 2\)

Suy ra \({x^2} - 3x - 2 = 0\).

Vì \(\Delta  = {( - 3)^2} - 4.( - 2) = 17 > 0\) nên phương trình có hai nghiệm phân biệt \({x_1};{x_2}\).

Áp dụng định lí Viète, ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} =  - \frac{{ - 3}}{1} = 3\\{x_1}{x_2} = \frac{{ - 2}}{1} =  - 2\end{array} \right.\).

Ta có:

\(\begin{array}{l}A = x_1^2 + x_2^2 - 5{x_1}{x_2}\\ = \left( {x_1^2 + 2{x_1}{x_2} + x_2^2} \right) - 7{x_1}{x_2}\\ = {\left( {{x_1} + {x_2}} \right)^2} - 7{x_1}{x_2}\\ = {3^2} - 7.\left( { - 2} \right)\\ = 23\end{array}\)

Vậy \(A = 23\)

Câu 5: (3,5 điểm) 1. Cho đường tròn (O) có bán kính bằng 3 cm. Từ điểm M nằm ngoài đường tròn (O) kẻ các tiếp tuyến MA, MB với (O) (A, B lần lượt là các tiếp điểm). Kẻ đường kính AC, tiếp tuyến tại C của (O) cắt AB tại D.

a) Chứng minh tứ giác OAMB nội tiếp.

b) Tính số đo của góc OCB, biết \(BC = 4\;{\rm{cm}}\).

c) Gọi N là giao điểm của MC và OD. Chứng minh \(\Delta MAC\) đồng dạng với \(\Delta CND\).

2. Một ly nước dạng hình nón có chiều cao 18cm, đường kính miệng ly 6cm. Lượng nước trong ly cao 12cm. Ly nước đặt cố định như hình vẽ (tức là hình nón đứng, đỉnh ở dưới). Tính thể tích phần nước trong ly.

Phương pháp:

1. a) Chứng minh \(\Delta MAO\) vuông tại A, \(\Delta MBO\) vuông tại B nên M, B, O cùng thuộc đường tròn đường kính OM nên M, O, A, B cùng thuộc đường tròn đường kính OM hay tứ giác OAMB nội tiếp.

b) Chứng minh \(\Delta ABC\) vuông tại B nên \(\cos OCB = \frac{{BC}}{{AC}}\) suy ra \(\angle OCB\)

c) Gọi H là giao điểm của OM và AB.

Chứng minh OM là trung trực của AB nên \(OM \bot AB\) tại trung điểm H của AB

Chứng minh $\Delta OAH\backsim \Delta OMA\left( g.g \right)$ suy ra \(O{A^2} = OH.OM\)

Kết hợp với \(OA = OC\) suy ra \(\frac{{OH}}{{OC}} = \frac{{OC}}{{OM}}\)

Chứng minh $\Delta OCH\backsim \Delta OMC\left( c.g.c \right)$ suy ra \(\angle OHC = \angle OCM\)

Chứng minh O, H, C, D cùng thuộc đường tròn đường kính OD

Suy ra \(\angle OCM = \angle ODC\)

Chứng minh \(\Delta CDN\) vuông tại N

Chứng minh $\Delta CDN\backsim \Delta MCA\left( g.g \right)$

2. Ta có hình nón lớn là cả ly có: chiều cao \(H = 18cm\) và bán kính đáy \(R = \frac{6}{2} = 3cm\)

Hình nón nhỏ bên trong là phần nước có: chiều cao \(h = 12cm\) và bán kính đáy \(r\)

Vì nước chiếm phần dưới của hình nón lớn, cùng hình dạng, nên hai hình nón đồng dạng, suy ra tỉ lệ các kích thước tương ứng bằng nhau. Tính r.

Tính thể tích phần nước bằng thể tích hình nón.

Lời giải:

1. a)

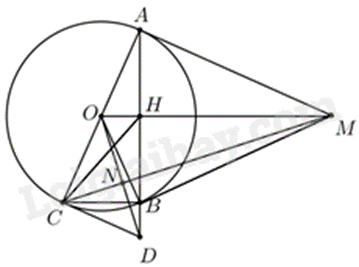
Do MA, MB là tiếp tuyến của (O) nên \(MA \bot OA,MB \bot OB\)

Khi đó \(\Delta MAO\) vuông tại A nên M, A, O cùng thuộc đường tròn đường kính OM

      \(\Delta MBO\) vuông tại B nên M, B, O cùng thuộc đường tròn đường kính OM

Vậy M, O, A, B cùng thuộc đường tròn đường kính OM hay tứ giác OAMB nội tiếp.

b) Ta có \(\angle ABC = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) nên \(\Delta ABC\) vuông tại B

Khi đó \(\cos OCB = \frac{{BC}}{{AC}} = \frac{4}{{2.3}} = \frac{2}{3}\) suy ra \(\angle OCB \approx 48,2^\circ \)

c)

Gọi H là giao điểm của OM và AB.

Ta có \(MA = MB\) (tính chất 2 tiếp tuyến cắt nhau) và \(OA = OB\) (cùng là bán kính)

Nên OM là trung trực của AB. Khi đó \(OM \bot AB\) tại trung điểm H của AB

Khi đó $\Delta OAH\backsim \Delta OMA\left( g.g \right)$ suy ra \(O{A^2} = OH.OM\)

Mà \(OA = OC\) nên \(O{C^2} = OH.OM\) suy ra \(\frac{{OH}}{{OC}} = \frac{{OC}}{{OM}}\)

Kết hợp \(\angle COM\) chung nên $\Delta OCH\backsim \Delta OMC\left( c.g.c \right)$

Suy ra \(\angle OHC = \angle OCM\)

Do \(\Delta OHD\) vuông tại H và \(\Delta OCD\) vuông tại C nên O, H, C, D cùng thuộc đường tròn đường kính OD

Suy ra \(\angle OHC = \angle ODC\). Suy ra \(\angle OCM = \angle ODC\)

Mà \(\angle OCM + \angle MCD = 90^\circ \) nên \(\angle ODC + \angle MCD = 90^\circ \) hay \(\Delta CDN\) vuông tại N

Xét \(\Delta CDN\) và \(\Delta MCA\) có \(\angle DNC = \angle MAC = 90^\circ \)

                     \(\angle ODC = \angle OCM\)

Suy ra $\Delta CDN\backsim \Delta MCA\left( g.g \right)$ (ĐPCM)

2. Ta có hình nón lớn là cả ly có: chiều cao \(H = 18cm\) và bán kính đáy \(R = \frac{6}{2} = 3cm\)

Hình nón nhỏ bên trong là phần nước có: chiều cao \(h = 12cm\) và bán kính đáy \(r\)

Vì nước chiếm phần dưới của hình nón lớn, cùng hình dạng, nên hai hình nón đồng dạng, suy ra tỉ lệ các kích thước tương ứng bằng nhau.

\(\begin{array}{l}\frac{r}{R} = \frac{h}{H} = \frac{{12}}{{18}} = \frac{2}{3}\\r = \frac{2}{3} \cdot 3 = 2{\mkern 1mu} cm\end{array}\)

Thể tích hình nón là \(V = \frac{1}{3}\pi {r^2}h\)

Áp dụng tính thể tích phần nước:

\(V = \frac{1}{3}\pi  \cdot {2^2} \cdot 12 = \frac{1}{3}\pi  \cdot 4 \cdot 12 = \frac{{48\pi }}{3} = 16\pi {\mkern 1mu} (c{m^3})\)

Câu 6: (1 điểm) Trong một cuộc thi tuyển dụng việc làm, ban tổ chức quy định mỗi người ứng tuyển phải trả lời 30 câu hỏi ở vòng sơ tuyển. Mỗi câu hỏi này có sẵn bốn đáp án, trong đó chỉ có một đáp án đúng. Người ứng tuyển chọn đáp án đúng sẽ được cộng thêm 2 điểm, chọn đáp án sai bị trừ 1 điểm. Ở vòng sơ tuyển, ban tổ chức tặng cho mỗi người dự thi 6 điểm và theo quy định người ứng tuyển phải trả lời hết 30 câu hỏi, người nào có số điểm từ 27 trở lên mới được dự thi vòng tiếp theo. Hỏi người ứng tuyển phải trả lời đúng ít nhất bao nhiêu câu hỏi ở vòng sơ tuyển thì mới được vào vòng tiếp theo?

Phương pháp:

Gọi x (câu) là số câu hỏi mà ứng viên phải trả lời đúng ở vòng sơ tuyển. \(\left( {0 \le x \le 30} \right)\)

Biểu diễn số câu trả lời sai theo x.

Chọn đáp án đúng sẽ được cộng thêm 2 điểm, chọn đáp án sai bị trừ 1 điểm, mỗi người dự thi sẽ được cộng 6 điểm nên số điểm của người ứng tuyển nên ta viết được biểu thức.

Vì số điểm từ 27 trở lên mới được dự thi vòng tiếp theo nên ta có bất phương trình.

Giải bất phương trình để tìm \(x\).

Lời giải:

Gọi x (câu) là số câu hỏi mà ứng viên phải trả lời đúng ở vòng sơ tuyển. \(\left( {0 \le x \le 30} \right)\)

Số câu trả lời sai: \(30 - x\) (câu)

Chọn đáp án đúng sẽ được cộng thêm 2 điểm, chọn đáp án sai bị trừ 1 điểm, mỗi người dự thi sẽ được cộng 6 điểm nên số điểm của người ứng tuyển là:

\(2x - \left( {30 - x} \right).1 + 6 = 2x - 30 + x + 6 = 3x - 24\) (điểm)

Số điểm từ 27 trở lên mới được dự thi vòng tiếp theo nên ta có:

\(3x - 24 \ge 27\)

\(\begin{array}{l}3x \ge 51\\x \ge 17\end{array}\)

Vậy người ứng tuyển phải trả lời đúng ít nhất 17 câu thì mới được vào vòng tiếp theo.