50 bài tập Tổng hợp hai dao động điều hòa cùng phương, cùng tần số - Phương pháp giản đồ Frenen mức độ thông hiểu

Câu hỏi 1 :

Phát biểu nào sau đây là sai khi nói về biên độ của dao động tổng hợp của hai dao động điều hoà cùng phương cùng tần số ?

A Phụ thuộc vào tần số của hai dao động thành phần.
B Phụ thuộc vào độ lệch pha của hai dao động thành phần.
C Lớn nhất khi hai dao động thành phần cùng pha
D Nhỏ nhất khi hai dao động thành phần ngược pha.

Đáp án: A

Lời giải chi tiết:

Đáp án A

Phương pháp: Sử dụng công thức tính biên độ của dao động tổng hợp hai dao động cùng phương, cùng tần số.

Đáp án - Lời giải

Câu hỏi 2 :

Biên độ dao động tổng hợp của hai dao động cùng phương, cùng tần số không phụ thuộc vào yếu tố nào sau đây?

A Biên độ dao động thứ nhất.
B Độ lệch pha của hai dao động.
C Biên độ dao động thứ hai.
D Tần số của hai dao động.

Đáp án: D

Phương pháp giải:

Phương pháp : Áp dụng công thức tính biên độ tổng hợp trong dao động điều hòa

$A = \sqrt {A_1^2 + A_2^2 + 2{A_1}{A_2}cos\varphi } $

Lời giải chi tiết:

Đáp án D

+ Biên độ của dao động tổng hợp không phụ thuộc vào tần số của hai dao động thành phần.

Đáp án - Lời giải

Câu hỏi 3 :

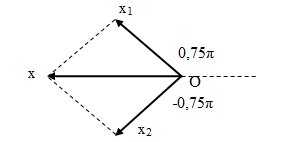
Xét 2 dao động điều hòa cùng phương, cùng tần số có phương trình dao đọng x₁ = 5cos(3πt + 0,75π)cm, x₂= 5sin(3πt – 0,25π)cm. Pha ban đầu của dao động tổng hợp là

A 0,5π
B 0
C -0,5π
D π

Đáp án: D

Phương pháp giải:

Phương pháp: Áp dụng công thức tính pha ban đầu của dao động tổng hợp

Lời giải chi tiết:

Đáp án D

x₁ = 5cos(3πt + 0,75π) cm

x₂ = 5sin(3πt – 0,25π) = 5cos(3πt – 0,75π) cm

Dao động tổng hợp có pha ban đầu φ được xác định:

$\tan \varphi = {{5.\sin (0,75\pi ) + 5\sin ( - 0,75\pi )} \over {5.c{\rm{os}}(0,75\pi ) + 5c{\rm{os}}( - 0,75\pi )}} = 0 \Rightarrow \left[ \matrix{
\varphi = 0 \hfill \cr
\varphi = \pi \hfill \cr} \right.$

Hình vẽ:

=> φ = π (rad)

Đáp án - Lời giải

Câu hỏi 4 :

Dao động của một vật là tổng hợp của hai dao động cùng phương có phương trình lần lượt là x₁= Acosωt và x₂ = Asinωt. Biên độ dao động của vật là

A $\sqrt 3A $
B A
C $\sqrt 2A $
D 2A

Đáp án: C

Phương pháp giải:

Sử dụng lí thuyết về tổng hợp hai dao động điều hoà

Lời giải chi tiết:

Theo đề bài ta có: x₁= Acosωt, x₂ = Asinωt = Acos(ωt – π/2) → hai dao động vuông pha với nhau

Do đó biên độ dao động tổng hợp: $A = \sqrt {{A_1}^2 + {A_2}^2} = A\sqrt 2 $

Đáp án - Lời giải

Câu hỏi 5 :

Cho hai dao động điều hòa cùng phương, cùng tần số, lệch pha nhau , pi/2 với biên độ A₁ và A₂. Dao động tổng hợp của hai dao động trên có biên độ là

A
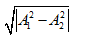
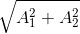
B $\sqrt{A_{1}^{2}+A_{2}^{2}}$
C A₁ + A₂
D

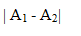
Đáp án: B

Lời giải chi tiết:

Đáp án - Lời giải

Câu hỏi 6 :

Một vật thực hiện đồng thời hai dao động điều hòa cùng phương cùng tần số có biên độ lần lượt là 6cm và 10cm. Biên độ dao động tổng hợp có thể là

A 2cm.
B 3cm.
C 5cm.
D 19cm.

Đáp án: C

Phương pháp giải:

Sử dụng điều kiện của biên độ dao động tổng hợp trong bài toán tổng hợp hai dao động điều hòa

Lời giải chi tiết:

Biên độ dao động tổng hợp phải thỏa mãn: $\left| {{A_1} - {A_2}} \right| \le A \le {A_1} + {A_2}$ → 4 ≤ A ≤ 16

=> Biên độ dao động tổng hợp có thể là 5cm

Đáp án - Lời giải

Câu hỏi 7 :

Hai dao động điều hòa cùng phương, cùng tần số có biên độ lần lượt là A₁= 8cm, A₂= 15cm và lệch pha nhau π/2. Dao động tổng hợp của hai dao động này có biên độ bằng.

A 7 cm.
B 23 cm.
C 17 cm.
D 11 cm.

Đáp án: C

Phương pháp giải:

Biên độ dao động tổng hợp của hai dao động cùng phương, cùng tần số, lệch pha π/2 : $A = \sqrt {{A_1}^2 + {A_2}^2} $

Lời giải chi tiết:

Do 2 dao động lệch pha góc π/2 => biên độ dao động tổng hợp:

$A = \sqrt {A_1^2 + A_2^2} = \sqrt {{8^2} + {{15}^2}} = 17(cm)$

Đáp án - Lời giải

Câu hỏi 8 :

Dao động của một vật là tổng hợp của hai dao động điều hoà cùng phương có phương trình ${x_1} = 3\cos (\omega t + \frac{\pi }{3})\;(cm)$ và ${x_2} = 4\cos (\omega t - \frac{{2\pi }}{3})\;(cm)$. Biên độ dao động tổng hợp của vật là

A 5 cm.
B 1 cm.
C 3 cm.
D 7 cm.

Đáp án: B

Phương pháp giải:

Áp dụng lí thuyết về tổng hợp hai dao động cùng tần số, ngược pha

Lời giải chi tiết:

PT hai dao động thành phần: ${x_1} = 3\cos (\omega t + \frac{\pi }{3})\;(cm)$và ${x_2} = 4\cos (\omega t - \frac{{2\pi }}{3})\;(cm)$

=> Hai dao động ngược pha

=> Biên độ dao động tổng hợp: $A = \left| {{A_1} - {A_2}} \right| = 1(cm)$ => Chọn B

Đáp án - Lời giải

Câu hỏi 9 :

Hai dao động điều hòa cùng phương, cùng tần số, ngược pha nhau có biên độ lần lượt là A₁ và A₂. Dao động tổng hợp của hai dao động này có biên độ là

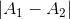
A $\left| {{A_1} - {A_2}} \right|$
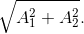
B $\sqrt {A_1^2 + A_2^2} .$
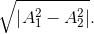
C $\sqrt {\left| {A_1^2 - A_2^2} \right|} .$
D ${A_1} + {A_2}$

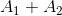
Đáp án: A

Lời giải chi tiết:

Đáp án A

Phương pháp : Biên độ dao động tổng hợp trong tổng hợp hai dao động điều hòa cùng phương, cùng tần số, ngược pha

Hai dao động điều hòa cùng phương, cùng tần số, ngược pha nhau có biên độ lần lượt là A₁ và A₂.

Dao động tổng hợp của hai dao động này có biên độ là: |A₁ – A₂|.

Đáp án - Lời giải

Câu hỏi 10 :

Hai dao động điều hòa lần lượt có phương trình x₁=A₁cos(20πt+π/2) cm và x₂=A₂cos(20πt+π/6) cm. Phát biểu nào sau đây là đúng?

A Dao động thứ hai sớm pha hơn dao động thứ nhất một góc π/4.
B Dao động thứ hai trễ pha hơn dao động thứ nhất một góc π/6.
C Dao động thứ nhất trễ pha hơn dao động thứ hai một góc π/3.
D Dao động thứ nhất sớm pha hơn dao động thứ hai một góc π/3.

Đáp án: D

Phương pháp giải:

Sử dụng mối quan hệ về pha giữa hai dao động điều hòa.

Lời giải chi tiết:

Hai phương trình dao động thành phần x₁ = A₁cos(20πt + π/2) cm và x₂ = A₂cos(20πt + π/6) cm

=> Dao động thứ nhất sớm pha hơn so với dao động thứ hai một góc π/3

=> Chọn đáp án D

Đáp án - Lời giải

Câu hỏi 11 :

Cho hai dao động điều hòa cùng phương, cùng tần số, lệch pha nhau 3π/2 rad với biên độ A₁ và A₂. Dao động tổng hợp của hai dao động có biên độ là

A $A = \sqrt {A_1^2 + A_2^2} $
B A = |A1-A2|
C $A = \sqrt {A_1^2 - A_2^2} $
D A = A₁ + A₂

Đáp án: A

Phương pháp giải:

Sử dụng lí thuyết về tổng hợp hai dao động điều hòa

Lời giải chi tiết:

Hai dao động điều hòa cùng phương, cùng tần số và lệch pha nhau góc 3π/2 rad

=> Hai dao động vuông pha => Biên độ dao động tổng hợp là $A = \sqrt {A_1^2 + A_2^2} $

=> Chọn đáp án A

Đáp án - Lời giải

Câu hỏi 12 :

Hai dao động điều hòa cùng phương, cùng tần số, lệch nhau một góc 0,5π, dọc theo trục tọa độ Ox. Các vị trí cân bằng cùng có tọa độ x = 0. Tại thời điểm t, li độ của các dao động lần lượt là x₁ = 4 cm và x₂ = 3 cm, khi đó li độ của dao động tổng hợp bằng

A 7cm
B 3cm
C 5cm
D 1cm

Đáp án: C

Phương pháp giải:

Áp dụng công thức tổng hợp dao động

Lời giải chi tiết:

Vì độ lệch pha giữa hai dao động là p/2 nên ta có công thức li độ tổng hợp là:

$x = \sqrt {x_1^2 + x_2^2} = \sqrt {{3^2} + {4^2}} = 5cm$

Chọn C

Đáp án - Lời giải

Câu hỏi 13 :

Một vật tham gia đồng thời hai dao động cùng phương, cùng tần số có biên độ lần lượt là A₁ = 3 cm và cm. Biên độ của dao động tổng hợp không thể nhận giá trị nào sau đây?.

A 5,7 cm.
B 1,0 cm.
C 7,5 cm
D 5,0 cm

Đáp án: C

Phương pháp giải:

Phương pháp: Tổng hợp dao động điều hóa

Lời giải chi tiết:

Đáp án C

+ Biên độ dao động tổng hợp A luôn thõa mãn $$\left| {{A_1} - {A_2}} \right| \le A \le {A_1} + {A_2}$$→ 1 cm ≤ A ≤ 7 cm.

→ A không thể nhận giá trị 7,5 cm.

Đáp án - Lời giải

Câu hỏi 14 :

Một vật thực hiện đồng thời hai ba dao động điều hòa cùng phương, cùng tần số có phương trình ${x_1} = 2\cos \left( {3t - {{2\pi } \over 3}} \right)cm$, ${x_2} = 2\cos \left( {3t} \right)cm$, ${x_3} = - 2{\rm{cos}}\left( {3t} \right) cm$. Phương trình dao động tổng hợp của vật là

A $x = 2\cos \left( {3t - {{2\pi } \over 3}} \right) cm$
B $x = 2\cos \left( {3t + {\pi \over 3}} \right) cm$
C $x = \sqrt 3 \cos \left( {3t + \pi } \right) cm$
D $x = 2\cos \left( {3t - {\pi \over 6}} \right) cm$

Đáp án: A

Lời giải chi tiết:

Đáp án A

+ Phương trình dao động tổng hợp $x = {x_1} + {x_2} + {x_3} = 2\cos \left( {3t - {{2\pi } \over 3}} \right) cm $

Đáp án - Lời giải

Câu hỏi 15 :

Hai dao động điều hòa cùng phương, cùng tần số, có các phương trình dao động là: ${x_1} = 3\cos \left( {\omega t - {\pi \over 4}} \right)(cm);{x_2} = 4\cos \left( {\omega t + {\pi \over 4}} \right)(cm)$ . Biên độ dao động tổng hợp của hai phương trình trên là:

A 5cm
B 12cm
C 7cm
D 1cm

Đáp án: A

Phương pháp giải:

Công thức tính biên độ dao động tổng hợp hai dao động điều hoà cùng phương, cùng tần số:

$A = \sqrt {A_1^2 + A_2^2 + 2{A_1}{A_2}c{\rm{os}}\Delta \varphi } $

Lời giải chi tiết:

Ta có: $A = \sqrt {A_1^2 + A_2^2 + 2{A_1}{A_2}c{\rm{os}}\Delta \varphi } = \sqrt {{3^2} + {4^2} + 2.3.4.c{\rm{os}}\left[ {{\pi \over 4} - \left( { - {\pi \over 4}} \right)} \right]} = 5cm$

Chọn A

Đáp án - Lời giải

Câu hỏi 16 :

Chuyển động của một vật là tổng hợp của hai dao động điều hòa cùng phương. Hai dao động này có phương trình lần lượt là ${x_1} = {A_1}\cos \left( {\omega t + {\pi \over 3}} \right) cm $ và ${x_2} = {A_2}\cos \left( {\omega t - {\pi \over 6}} \right) cm $. Biên độ dao động của vật là :

A $\sqrt {A_1^2 + A_2^2} $
B $\left| {{A_1} - {A_2}} \right|$
C A₁ + A₂.
D ${{{A_1} + {A_2}} \over 2}$

Đáp án: A

Phương pháp giải:

Phương pháp: Tổng hợp dao động điều hòa

Lời giải chi tiết:

Đáp án A

+ Biên độ tổng hợp của hai dao động vuông pha $\sqrt {A_1^2 + A_2^2} $

Đáp án - Lời giải

Câu hỏi 17 :

Hai dao động điều hòa cùng phương, cùng tần số có biên độ lần lượt là A₁= 3cm, A₂= 4cm và lệch pha nhau ${\pi \over 2}$. Dao động tổng hợp của hai dao động này có biên độ bằng:

A $3\sqrt 2 cm$
B 3,2cm
C 5cm
D 7cm

Đáp án: C

Phương pháp giải:

Công thức tính biên độ dao động tổng hợp: $A = \sqrt {A_1^2 + A_2^2 + 2{A_1}{A_2}c{\rm{os}}\Delta \varphi } $

Lời giải chi tiết:

Biên độ dao động tổng hợp: $A = \sqrt {{3^2} + {4^2} + 2.3.4.c{\rm{os}}{\pi \over 2}} = 5cm$

Chọn C

Đáp án - Lời giải

Câu hỏi 18 :

Cho hai dao động điều hòa cùng phương có các phương trình lần lượt là ${x_1} = 4\cos \left( {\pi t - {\pi \over 6}} \right)cm$ và ${x_2} = 4\cos \left( {\pi t - {\pi \over 2}} \right)\,cm$. Dao động tổng hợp của hai dao động này có biên độ là

A 2cm.
B $4\sqrt 3 cm $
C $4\sqrt 2 cm $
D 8 cm.

Đáp án: B

Phương pháp giải:

Phương pháp: Áp dụng công thức tính biên độ tổng hợp trong dao động điều hòa $A = \sqrt {A_1^2 + A_2^2 + 2{A_1}{A_2}\cos \Delta \varphi } .$

Lời giải chi tiết:

Đáp án B

+ Biên độ của hai dao động tổng hợp $A = \sqrt {A_1^2 + A_2^2 + 2{A_1}{A_2}\cos \Delta \varphi } = \sqrt {{4^2} + {4^2} + 2.4.4.\cos \left( {{\pi \over 3}} \right)} = 4\sqrt 3 \,\,cm.$

Đáp án - Lời giải

Câu hỏi 19 :

Một vật tham gia đồng thời hai dao động điều hoà cùng phương, có phương trình lần lượt là x₁ = 3sin(10t + π/3) cm và x₂ = 4cos(10t – π/6) cm. Biên độ dao động tổng hợp của vật là

A 1 cm
B 5 cm
C 5 mm
D 7 cm

Đáp án: D

Phương pháp giải:

Sử dụng máy tính casio.

Lời giải chi tiết:

Ta có x₁ = 3sin(10t + π/3) = 3cos(10t – π/6) cm

Cài đặt máy tính ở chế độ số phức MODE 2

Ta có x = x₁ + x₂, bấm máy

$3\angle - {\pi \over 6} + 4\angle - {\pi \over 6}SHIFT23 = $

Đọc kết quả $7\angle - {\pi \over 6}$

Vậy dao động tổng hợp có biên độ là 7 cm

Chọn D

Đáp án - Lời giải

Câu hỏi 20 :

Một vật tham gia đồng thời hai dao động điều hoà cùng phương, có phương trình lần lượt là x₁ = 3cos(20t +π/3) cm và x₂ = 4cos(20t – π/6) cm. Biên độ dao động tổng hợp của vật là

A 1 cm
B 5 cm
C 5 mm
D 7 cm

Đáp án: B

Phương pháp giải:

Sử dụng máy tính casio.

Lời giải chi tiết:

Cài đặt máy tính ở chế độ số phức MODE 2

Ta có x = x₁ + x₂, bấm máy

$3\angle {\pi \over 3} + 4\angle - {\pi \over 6}SHIFT23 = $

Đọc kết quả $5\angle 0,1199$

Vậy dao động tổng hợp có biên độ 5 cm

Chọn B

Đáp án - Lời giải

Câu hỏi 21 :

Hai dao động cơ điều hoà có cùng phương và cùng tần số f = 50 Hz, có biên độ lần lượt là 2A và A, pha ban đầu lần lượt là π/3 và π. Phương trình của dao động tổng hợp có thể là phương trình nào sau đây:

A x = A$\sqrt3$cos(100πt +π/2)
B x = 3Acos(100πt + π/2)
C x = A$\sqrt3$cos(100πt - π/2)
D x = 3Acos(100πt + π/2)

Đáp án: A

Phương pháp giải:

Sử dụng máy tính casio.

Lời giải chi tiết:

Tần số góc ω = 2πf = 100π rad/s

Cài đặt máy tính ở chế độ số phức MODE 2

Ta có x = x₁ + x₂, bấm máy

$2\angle {\pi \over 3} + 1\angle \pi SHIFT23 = $

Đọc kết quả $\sqrt 3 \angle {\pi \over 2}$

Vậy PT dao động tổng hợp là $x = \sqrt 3 A\cos \left( {100\pi t + {\pi \over 2}} \right)cm$

Chọn A

Đáp án - Lời giải

Câu hỏi 22 :

Một vật thực hiện đồng thời hai dao động điều hòa cùng phương theo các phương trình x₁ = - 4sin(πt) cm và x₂ = 4$\sqrt3$cosπt cm. Phương trình dao động tổng hợp là

A x = 8cos(πt + π/6) cm
B x = 8sin(πt – π/6) cm
C x = 8cos(πt – π/6) cm
D x = 8sin(πt + π/6) cm

Đáp án: A

Phương pháp giải:

Sử dụng máy tính casio.

Lời giải chi tiết:

Ta có x₁ = -4sinπt = 4cos(πt + π/2) cm

Cài đặt máy tính ở chế độ số phức MODE 2

Ta có x = x₁ + x₂, bấm máy

$4\angle {\pi \over 2} + 4\sqrt 3 \angle 0SHIFT23 = $

Đọc kết quả $8\angle {\pi \over 6}$

Vậy phương trình dao động tổng hợp là x = 8cos(πt + π/6) cm

Chọn A

Đáp án - Lời giải

Câu hỏi 23 :

Một vật tham gia hai dao động điều hoà cùng phương cùng tần số có các phương trình lần lượt là x₁ = 5sin(ωt – π/3) cm; x₂ = 5sin(ωt + 5π/3) cm. Dao động tổng hợp có dạng

A x=5 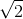${\sqrt{2}}$ cos(ωt+π/3)cm.
B x=10cos(ωt-π/3)cm.
C x=5 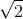${\sqrt{2}}$ sin(ωt) cm.
D x= 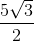$\frac{5\sqrt{3}}{2}$ cos(ωt+π/3) cm.

Đáp án: B

Phương pháp giải:

Sử dụng máy tính casio.

Lời giải chi tiết:

Cài đặt máy tính ở chế độ số phức MODE 2

Ta có x = x₁ + x₂, bấm máy

$5\angle - {\pi \over 3} + 5\angle {{5\pi } \over 3}SHIFT23 = $

Đọc kết quả $10\angle - {\pi \over 3}$

Vậy phương trình dao động tổng hợp của vật là x = 10sin(ωt – π/3) rad

Chọn B

Đáp án - Lời giải

Câu hỏi 24 :

Một vật đồng thời tham gia 3 dao động cùng phương, cùng tần số có phương trình dao động: x₁ = 8cos(2πt + π/2) (cm), x₂ = 2cos(2πt -π/2) (cm) và x₃ = A₃ cos(πt +φ₃) (cm). Phương trình dao động tổng hợp có dạng x = 6 cos(2πt + π/4) (cm). Tính biên độ dao động và pha ban đầu của dao động thành phần thứ 3:

A 4,59cm và –π/8 rad
B 6cm và π/3.
C 8cm và π/6.
D 8cm và π/2.

Đáp án: A

Phương pháp giải:

Sử dụng máy tính casio.

Lời giải chi tiết:

Cài đặt máy tính ở chế độ số phức MODE 2

Ta có x₃ = x – x₁ – x₂

Bấm máy $6\angle {\pi \over 4} - 8\angle {\pi \over 2} - 2\angle - {\pi \over 2}SHIFT23 = $

Đọc kết quả $4,59\angle - {\pi \over 8}$

Vậy biên độ và pha ban đầu của dao động thành phần thứ 3 là 4,59 cm và –π/8 rad

Đáp án - Lời giải

Câu hỏi 25 :

Hai chất điểm chuyển động trên hai quỹ đạo song song, cạnh nhau, cùng gốc toạ độ với các phương trình x₁ = 3coswt (cm) và x₂ = 4sinwt (cm). Khi hai chất điểm ở xa nhau nhất thì chất điểm 1 có li độ

A ± 1,8 cm.
B ±3 cm.
C 0 cm.
D ±3,2 cm.

Đáp án: A

Phương pháp giải:

Sử dụng máy tính casio.

Lời giải chi tiết:

Ta có x₂ = 4sinωt = 4cos(ωt – π/2) cm

Khoảng cách giữa hai dao động theo phương Ox

$d = \left| {{x_2} - {x_1}} \right|$

Cài đặt máy tính ở chế độ số phức MODE 2

Bấm máy $4\angle - {\pi \over 2} - 3\angle 0SHIFT23 = $

Đọc kết quả $5\angle - 2,2$

Vậy khoảng cách giữa hai vật theo phương Ox là $d = \left| {5\cos \left( {\omega t - 2,2} \right)} \right|$

Khi hai vật ở xa nhau nhất => d = 5cm

Khi đó, x₁ = ±1,8 cm

Chọn A

Đáp án - Lời giải

Câu hỏi 26 :

Một vật thực hiện đồng thời hai dao động điều hoà cùng phương, cùng tần số có phương trình dao động là ${{\rm{x}}_1} = \sqrt 2 \cos \left( {2t + {\pi \over 3}} \right)cm$ và ${x_2} = \sqrt 2 \cos \left( {2t - {\pi \over 6}} \right)cm$ . Phương trình dao động tổng hợp là

A $x = \sqrt 2 \cos \left( {2t + {\pi \over 6}} \right)cm$
B x =2cos(2t + π/12)(cm).
C $x = 2\sqrt 3 \cos \left( {2t + {\pi \over 3}} \right)cm$
D x =2cos(2t - π/6)(cm)

Đáp án: B

Phương pháp giải:

Sử dụng máy tính casio.

Lời giải chi tiết:

Cài đặt máy tính ở chế độ số phức MODE 2

Ta có x = x₁ + x₂, bấm máy

$\sqrt 2 \angle {\pi \over 3} + \sqrt 2 \angle - {\pi \over 6}SHIFT23 = $

Đọc kết quả $2\angle {\pi \over {12}}$

Vậy phương trình dao động tổng hợp là x = 2cos(2t + π/12) cm

Chọn B

Đáp án - Lời giải

Câu hỏi 27 :

Một vật thực hiện đồng thời 3 dao động điều hoà cùng phương, cùng tần số f = 5Hz. Biên độ dao động và pha ban đầu của các dao động thành phần lần lượt là A₁ = 433mm, A₂ = 150mm, A₃ = 400mm; $\varphi = 0,\varphi = {\pi \over 2},\varphi = {{ - \pi } \over 2}$ . Dao động tổng hợp có phương trình dao động là

A x = 500cos(10πt + π/6)(mm).
B x = 500cos(10πt - π/6)(mm).
C x = 50cos(10πt + π/6 )(mm).
D x = 500cos(10πt - π/6)(cm).

Đáp án: B

Phương pháp giải:

Sử dụng máy tính casio.

Lời giải chi tiết:

Tần số góc ω = 2πf = 10Hz

Cài đặt máy tính ở chế độ số phức MODE 2

Ta có x = x₁ + x₂ + x₃, bấm máy

$433\angle 0 + 150\angle {\pi \over 2} + 400\angle - {\pi \over 2}SHIFT23 = $

Đọc kết quả $499,99\angle - 0,5236$

Thấy rằng kết quả này gần nhất với $500\angle - {\pi \over 6}$

Vậy phương trình dao động tổng hợp là x = 500cos(10πt - π/6)(mm).

Chọn B

Đáp án - Lời giải

Câu hỏi 28 :

Ba con lắc lò xo 1, 2, 3 đặt thẳng đứng cách đều nhau theo thứ tự 1, 2, 3. Ở vị trí cân bằng ba vật có cùng độ cao. Con lắc thứ nhất dao động có phương trình x₁ = 3cos(20πt + π/2) (cm), con lắc thứ hai dao động có phương trình x₂ = 1,5cos(20πt) (cm). Hỏi con lắc thứ ba dao động có phương trình nào thì ba vật luôn luôn nằm trên một đường thẳng?

A x₃ = 3$\sqrt3$cos(20πt – π/4) (cm).
B x₃ = 2cos(20πt – π/4) (cm).
C x₃ = 3$\sqrt3$cos(20πt – π/2) (cm).
D x₃ = 3$\sqrt3$cos(20πt + π/4) (cm).

Đáp án: A

Phương pháp giải:

Sử dụng máy tính casio.

Lời giải chi tiết:

Để ba vật luôn nằm trên cùng một đường thẳng trong quá trình vật dao động thì ${{\rm{x}}_2} = {{{x_1} + {x_3}} \over 2} \Rightarrow {x_3} = 2{{\rm{x}}_2} - {x_1}$

Cài đặt máy tính ở chế độ số phức MODE 2

Bấm máy $2.1,5\angle 0 - 3\angle {\pi \over 2}SHIFT23 = $

Đọc kết quả $3\sqrt 2 \angle - {\pi \over 4}$

Vậy phương trình dao động của con lắc thứ ba là ${x_3} = 3\sqrt 2 \cos \left( {20\pi t - {\pi \over 4}} \right)cm$

Chọn A

Đáp án - Lời giải

Câu hỏi 29 :

Cho hai dao động điều hoà cùng phương, cùng tần số và vuông pha với nhau. Khi dao động thứ nhất có li độ 4cm thì li độ dao động thứ hai là -3cm. Li độ của dao động tổng hợp của hai dao động trên bằng:

A 5cm
B 7cm
C 1cm
D 0,5cm

Đáp án: C

Phương pháp giải:

Phương pháp: x = x₁ + x₂

Lời giải chi tiết:

Cách giải:

Li độ của dao động tổng hợp x = x₁ + x₂ = 4 + (-3) = 1cm

Đáp án C

Đáp án - Lời giải

Câu hỏi 30 :

Hai dao động điều hòa, cùng phương, cùng tần số, ngược pha, có biên độ lần lượt là A₁, A₂. Biên độ dao động tổng hợp của hai dao động này là

A ${A_1} + {A_2}$
B $\left| {{A_1} - {A_2}} \right|$
C $\sqrt {\left| {A_1^2 - A_2^2} \right|} .$
D $\sqrt {A_1^2 + A_2^2} .$

Đáp án: B

Lời giải chi tiết:

Đáp án B

Vì haidao động điều hòa dao động cùng phương cùng tần số nhưng ngược pha nên biên độ tổng hợp được xác định bởi biểu thức $\left| {{A_1} - {A_2}} \right|$

Đáp án - Lời giải

Câu hỏi 31 :

Hai dao động điều hòa cùng phương, cùng tần số nhưng vuông pha. Tại thời điểm t giá trị tức thời của hai li độ là 6cm và 8cm Giá trị của li độ tổng hợp tại thời điểm đó là:

A 10cm
B 14cm
C 2cm
D 12cm

Đáp án: B

Lời giải chi tiết:

Giá trị của li độ tổng hợp : x = 6 + 8 = 14 cm

Đáp án - Lời giải

Câu hỏi 32 :

Một vật tham gia đồng thời hai dao động điều hòa cùng phương có phương trình lần lượt là x₁ = 5cos(10πt – 0,5π)cm và x₂ = 10cos(10πt + 0,5π)cm. Vận tốc cực đại của vật là

A 100π cm/s
B 10π cm/s
C 25π cm/s
D 50π cm/s

Đáp án: D

Phương pháp giải:

tổng hợp dao động

Lời giải chi tiết:

Hai dao động ngược pha nên dao động tổng là:

$\begin{gathered}
x = 5.\cos \left( {10\pi t + 0,5\pi } \right) \hfill \\
= > {v_{\max }} = \omega A = 5.10\pi = 50\pi cm/s \hfill \\
\end{gathered} $

Đáp án - Lời giải

Câu hỏi 33 :

Hai dao động điều hòa cùng phương, có phương trình x₁ = 3cos(20πt) cm và x₂ = 4cos(20πt + 0,5π). Dao động tổng hợp của hai dao động này có biên độ là

A 4 cm.
B 8 cm.
C 5 cm.
D 2 cm.

Đáp án: C

Phương pháp giải:

Sử dụng lí thuyết về tổng hợp hai dao động điều hòa cùng tần số

Lời giải chi tiết:

Hai dao động x₁ và x₂ vuông pha với nhau

Biên độ dao động được tính theo công thức $A = \sqrt {A_1^2 + A_2^2} = \sqrt {{3^2} + {4^2}} = 5cm$

Chọn C

Đáp án - Lời giải

Câu hỏi 34 :

dao động của vật là tổng hợp của hai dao động điều hòa cùng phương có phương trình lần lượt là

${x_1} = 8\sin (\pi t + \alpha )(cm)$

và

${x_2} = 4\cos (\pi t)(cm)$

. Biên độ dao động của vật bằng 12cm thì

A
$\alpha = \pi $ rad
B
$\alpha = - \frac{\pi }{2}$rad
C α =0 rad
D
$\alpha = \frac{\pi }{2}$rad

Đáp án: D

Phương pháp giải:

tổng hợp hai dao động bằng đại số

Lời giải chi tiết:

Ta có :

$\begin{gathered}
{x_1} = 8\sin (\pi t + \alpha ) = 8\cos (\pi t + \alpha - \frac{\pi }{2}) \hfill \\
{x_2} = 4\cos \pi t \hfill \\
\end{gathered} $

Để biên độ dao động tổng hợp A = 12 thì hai dao động phải cùng pha nên :

$\alpha - \frac{\pi }{2} = 0 \Leftrightarrow \alpha = \frac{\pi }{2}$

Đáp án - Lời giải

Câu hỏi 35 :

Một vật tham gia đồng thời vào hai dao động điều hòa cùng tần số góc 10 rad/s, có biên độ lần lượt là 6 cm và 8 cm. Tốc độ cực đại của vật không thể là

A 15 cm/s .
B 50 cm/s.
C 60 cm/s.
D 30 cm/s.

Đáp án: A

Lời giải chi tiết:

Đáp án A

+ Ta có biên độ dao động tổng hợp A có khoảng giá trị: $8 - 6 = 2\,\,cm \le A \le 8 + 6 = 15\,\,cm$.

$ \to $ khoảng giá trị của tốc độ cực đại: $20\,\,{{cm} / s} \le 150\,\,{{cm} / s}$

$ \to {v_{\max }}$ không thể là $15\,\,{cm/ s}$

Đáp án - Lời giải

Câu hỏi 36 :

Chuyển động của một vật là tổng hợp của hai dao động điều hòa cùng phương. Hai dao động này có phương trình lần lượt là ${x_1} = 4\cos (10t + \frac{\pi }{4})$ (cm) và ${x_2} = 3\cos (10t - \frac{{3\pi }}{4})$ (cm). Độ lớn vận tốc của vật ở vị trí cân bằng là

A 100 cm/s.
B 50 cm/s.
C 80 cm/s.
D 10 cm/s.

Đáp án: D

Phương pháp giải:

Phương pháp: Độ lớn vận tốc ở vị trí cân bằng v_max = ωA

Lời giải chi tiết:

Đáp án D

Cách giải:

Hai dao động: ${x_1} = 4\cos (10t + \frac{\pi }{4})cm;{x_2} = 3\cos (10t - \frac{{3\pi }}{4})cm $dao động ngược pha

=> Biên độ của dao động tổng hợp: A = |A₁ – A₂| = |4 – 3| = 1cm

=> Độ lớn vận tốc của vật ở vị trí cân bằng là: v_max = ωA = 10.1 = 10 (cm/s)

Đáp án - Lời giải

Câu hỏi 37 :

Một vật nhỏ có khối lượng m thực hiện đồng thời hai dao động điều hòa cùng phương, cùng tần số góc ω, ngược pha với nhau và có các biên độ thành phần lần lượt là A₁, A₂. Cơ năng của vật là

A ${1 \over 2}m{\omega ^2}\left( {A_1^2 + A_2^2 + {A_1}{A_2}} \right)$
B ${1 \over 2}m{\omega ^2}{\left( {{A_1} + {A_2}} \right)^2}$
C ${1 \over 2}m{\omega ^2}\left( {A_1^2 + A_2^2} \right)$
D ${1 \over 2}m{\omega ^2}{\left( {{A_1} - {A_2}} \right)^2}$

Đáp án: D

Phương pháp giải:

Sử dụng lí thuyết về tổng hợp hai dao động điều hòa cùng tần số

Lời giải chi tiết:

Vì hai dao động ngược pha với nhau nên biên độ dao động tổng hợp được tính theo công thức

$A = \left| {{A_1} - {A_2}} \right|$

Cơ năng của vật được tính theo công thức

${\rm{W = }}{1 \over 2}m{\omega ^2}{A^2} = {1 \over 2}m{\omega ^2}{\left( {{A_1} - {A_2}} \right)^2}$

Chọn đáp án D

Đáp án - Lời giải

Câu hỏi 38 :

Một vật tham gia đồng thời hai dao động điều hòa, cùng phương, cùng tần số có phương trình x₁= -2.cos (2πt) cm và ${x_2} = 2\sin \left( {2\pi t + \frac{\pi }{6}} \right)cm$. Tốc độ dao động cực đại của vật là

A 12,57 cm/s
B 21,77 cm/s
C 24,25 cm/s
D 6,53 cm/s

Đáp án: A

Phương pháp giải:

Tổng hợp hai dao động điều hòa và tính vận tốc cực đại

Lời giải chi tiết:

Biến đổi hai dao động thành phần ta được

$\begin{array}{l}
{x_1} = - 2\cos \left( {2\pi t} \right) = 2\cos \left( {2\pi t + \pi } \right)\\
{x_2} = 2\sin (2\pi t + \frac{\pi }{6}) = 2\cos \left( {2\pi t + \frac{\pi }{6} - \frac{\pi }{2}} \right)cm\\
x = {x_1} + {x_2} = 2\cos \left( {2\pi t - \frac{{2\pi }}{3}} \right)cm\\
= > {v_{\max }} = \omega .A = 2\pi .2 = 4\pi = 12,57cm/s
\end{array}$

Đáp án - Lời giải

Câu hỏi 39 :

Cho hai dao động điều hòa cùng phương có các phương trình lần lượt là ${{\text{x}}_{\text{1}}}\text{= 4cos}\left( \text{ }\!\!\pi\!\!\text{ t - }\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}} \right)\text{ (cm)}$ và ${{\text{x}}_{2}}\text{= 4cos}\left( \text{ }\!\!\pi\!\!\text{ t - }\frac{\text{ }\!\!\pi\!\!\text{ }}{2} \right)\text{ (cm)}$. Dao động tổng hợp của hai dao động này có biên độ là

A 2 cm
B $\text{4}\sqrt{\text{2}}\text{ cm}$
C 8 cm
D $\text{4}\sqrt{\text{3}}\text{ cm}$

Đáp án: D

Phương pháp giải:

Áp dụng công thức tính biên độ của dao động tổng hợp:

${{\text{A}}^{\text{2}}}\text{ = A}_{\text{1}}^{\text{2}}\text{ + A}_{\text{2}}^{\text{2}}\text{ + 2}{{\text{A}}_{\text{1}}}{{\text{A}}_{\text{2}}}\text{cos (}{{\text{ }\!\!\varphi\!\!\text{ }}_{\text{1}}}-{{\text{ }\!\!\varphi\!\!\text{ }}_{\text{2}}}\text{)}$

Lời giải chi tiết:

Ta có: ${{\text{A}}^{\text{2}}}\text{ = A}_{\text{1}}^{\text{2}}\text{ + A}_{\text{2}}^{\text{2}}\text{ + 2}{{\text{A}}_{\text{1}}}{{\text{A}}_{\text{2}}}\text{cos (}{{\text{ }\!\!\varphi\!\!\text{ }}_{\text{1}}}-{{\text{ }\!\!\varphi\!\!\text{ }}_{\text{2}}}\text{) = 48}$

$\Rightarrow \text{A = 4}\sqrt{\text{3}}\text{ (cm)}$

Chọn D

Đáp án - Lời giải

Câu hỏi 40 :

Cho hai dao động cùng phương: x₁ = 3cos(ωt + φ₁ ) cm và x₂ = 4cos ωt + φ₂ )cm. Biết hợp của hai dao động trên có biên độ bằng 5 cm. Chọn hệ thức đúng giữa φ₁ và φ₂.

A φ₂ - φ₁ = 2kπ.
B φ₂ - φ₁ = (2k + 1)π/4.
C φ₂ - φ₁ = (2k + 1)π/2.
D φ₂ - φ₁ = (2k + 1)π.

Đáp án: C

Phương pháp giải:

Áp dụng lí thuyết về tổng hợp hai dao động điều hòa

Lời giải chi tiết:

Ta thấy rằng nên hai dao động thành phần vuông pha với nhau

Do đó φ₂ - φ₁ = (2k + 1)π/2

Chọn đáp án C

Đáp án - Lời giải

Câu hỏi 41 :

Hai dao động cùng phương có phương trình lần lượt là ${x_1} = {A_1}\cos \left( {\omega t + {\varphi _1}} \right)$ và ${x_2} = {2_1}\cos \left( {\omega t + {\varphi _2}} \right)$. Gọi A là biên độ dao động tổng hợp của hai dao động trên. Hệ thức nào sau đây luôn đúng?

A $A = {A_1} + {A_2}$
B ${A_1} + {A_2} \ge A \ge \left| {{A_1} - {A_2}} \right|$
C $A = \left| {{A_1} - {A_2}} \right|$
D $A = \sqrt {A_1^2 + A_2^2} $

Đáp án: B

Phương pháp giải:

Biên độ của dao động tổng hợp: $A = \sqrt {A_1^2 + A_2^2 + 2{A_1}{A_2}.cos\Delta \varphi } $

Lời giải chi tiết:

Khi $\left\{ \begin{array}{l}\Delta \varphi = 2k\pi \Rightarrow {A_{\max }} = {A_1} + {A_2}\\\Delta \varphi = \left( {2k + 1} \right)\pi \Rightarrow {A_{\min }} = \left| {{A_1} - {A_2}} \right|\end{array} \right.$$ \Rightarrow {A_1} + {A_2} \ge A \ge \left| {{A_1} - {A_2}} \right|$

Chọn B.

Đáp án - Lời giải

Câu hỏi 42 :

Một vật thực hiện đồng thời hai dao động điều hòa cùng phương, có phương trình lần lượt là ${x_1} = 3cos\left( {\omega t} \right)\left( {cm} \right)$ và ${x_2} = 6cos\left( {\omega t - \pi } \right)\left( {cm} \right)$. Biên độ dao động tổng hợp của vật là

A $12cm.$
B $6cm.$
C $3cm.$
D $9cm.$

Đáp án: C

Phương pháp giải:

Sử dụng biểu thức tính biên độ dao động tổng hợp: ${A^2} = A_1^2 + A_2^2 + 2{A_1}{A_2}cos\Delta \varphi $

Lời giải chi tiết:

Ta có độ lệch pha giữa 2 dao động $\Delta \varphi = \pi \Rightarrow $ Hai dao động ngược pha nhau

$ \Rightarrow $ Biên độ dao động tổng hợp: $A = \left| {{A_1} - {A_2}} \right| = 3cm$

Chọn C

Đáp án - Lời giải

Câu hỏi 43 :

Hai dao động điều hòa cùng phương, có phương trình lần lượt là:

${x_1} = A.\cos \left( {\omega t + \frac{\pi }{3}} \right);{x_2} = A.\cos \left( {\omega t - \frac{{2\pi }}{3}} \right)$ là hai dao động:

A Lệch pha $\frac{\pi }{3}$
B Lệch pha $\frac{\pi }{2}$
C Ngược pha
D Cùng pha.

Đáp án: C

Phương pháp giải:

Độ lệch pha của hai dao động được xác định $\Delta \varphi = {\varphi _1} - {\varphi _2}$

Lời giải chi tiết:

Ta có:

$\left\{ \begin{array}{l}
{x_1} = A.\cos \left( {\omega t + \frac{\pi }{3}} \right)\\
{x_2} = A.\cos \left( {\omega t - \frac{{2\pi }}{3}} \right)
\end{array} \right.$

Độ lệch pha của hai dao động là :

$\Delta \varphi = \frac{\pi }{3} - \left( { - \frac{{2\pi }}{3}} \right) = \pi $

Vậy hai dao động ngược pha.

Chọn C.

Đáp án - Lời giải

Câu hỏi 44 :

Cho hai đao động điều hòa có phương trình${x_1} = A.cos\left( {\omega t + 0,5\pi } \right);{\rm{ }}{x_2} = A.cos\left( {\omega t - 0,25\pi } \right).$ Độ lệch pha của hai đao động này là

A $0,5\pi $
B $0,25\pi $
C $ - 0,25\pi $
D $0,75\pi $

Đáp án: D

Phương pháp giải:

Độ lệch pha của hai dao động: $\Delta \varphi = \left| {{\varphi _1}-{\varphi _2}} \right|$

Lời giải chi tiết:

Độ lệch pha của hai dao động này là:

$\Delta \varphi = \left| {{\varphi _1}-{\varphi _2}} \right| = \left| {0,5\pi -\left( { - 0,25\pi } \right)} \right| = 0,75\pi $

Chọn D.

Đáp án - Lời giải

Câu hỏi 45 :

Nhận xét nào sau đây về biên độ dao động tổng hợp là không đúng? Dao động tổng hợp của hai dao động điều hòa cùng phương, cùng tần số có biên độ phụ thuộc

A vào biên độ của dao động thành phần thứ nhất
B Vào độ lệch pha giữa hai dao động thành phần
C vào biên độ của dao động thành phần thứ hai
D vào tần số của hai dao động thành phần

Đáp án: D

Phương pháp giải:

Áp dụng phương pháp tổng hợp hai dao động điều hòa bằng phương pháp freshnel

Lời giải chi tiết:

Ta có:

${A^2} = A_1^2 + A_2^2 + 2{A_1}{A_2}.\cos \Delta \varphi $

Biên độ của dao động tổng hợp của hai dao động điều hòa không phụ thuộc vào tần số của hai dao động.

Đáp án - Lời giải

Câu hỏi 46 :

Xét hai dao động điều hòa cùng phương, cùng tần số, độ lệch pha không đổi theo thời gian. Dao động thứ nhất có biên độ ${A_1}$ và pha ban đầu ${\varphi _1}$, dao động thứ hai có biên độ ${A_2}$ và pha ban đầu ${\varphi _2}$. Pha ban đầu của dao động tổng hợp xác định bởi công thức

A $\tan \varphi = \dfrac{{{A_1}cos{\varphi _1} + {A_2}cos{\varphi _2}}}{{{A_1}\sin {\varphi _1} + {A_2}\sin {\varphi _2}}}.$
B $\tan \varphi = \dfrac{{{A_1}\sin {\varphi _1} + {A_2}\sin {\varphi _2}}}{{{A_1}cos{\varphi _1} + {A_2}cos{\varphi _2}}}.$
C $\tan \varphi = \dfrac{{{A_1}\sin {\varphi _2} + {A_2}\sin {\varphi _1}}}{{{A_1}cos{\varphi _2} + {A_2}cos{\varphi _1}}}.$
D $\tan \varphi = \dfrac{{{A_1}cos{\varphi _2} + {A_2}\sin {\varphi _1}}}{{{A_1}cos{\varphi _2} + {A_2}\sin {\varphi _1}}}.$

Đáp án: B

Phương pháp giải:

Sử dụng biểu thức tính pha ban đầu của dao động tổng hợp

Lời giải chi tiết:

Pha ban đầu của dao động tổng hợp được xác định bởi biểu thức:

$\tan \varphi = \dfrac{{{A_1}\sin {\varphi _1} + {A_2}\sin {\varphi _2}}}{{{A_1}cos{\varphi _1} + {A_2}cos{\varphi _2}}}$

Chọn B

Đáp án - Lời giải

Câu hỏi 47 :

Hai dao động điều hòa cùng phương, cùng tần số, lệch nhau một góc 0,5π, dọc theo trục tọa độ Ox. Các vị trí cân bằng cùng có tọa độ x = 0. Tại thời điểm t, li độ của các dao động lần lượt là x₁ = 4 cm và x₂ = 3 cm, khi đó li độ của dao động tổng hợp bằng

A 7cm
B 3cm
C 5cm
D 1cm

Đáp án: C

Phương pháp giải:

Áp dụng công thức tổng hợp dao động

Lời giải chi tiết:

Vì độ lệch pha giữa hai dao động là p/2 nên ta có công thức li độ tổng hợp là:

$x = \sqrt {x_1^2 + x_2^2} = \sqrt {{3^2} + {4^2}} = 5cm$

Chọn C

Đáp án - Lời giải

Câu hỏi 48 :

Một vật thực hiện đồng thời hai dao động điều hòa cùng phương, lệch pha nhau $\dfrac{\pi }{2}$ và có biên độ lần lượt là 9 cm và 12 cm. Biên độ dao động của vật là

A 15cm
B 3cm
C 21cm
D 10,5cm

Đáp án: A

Phương pháp giải:

Sử dụng biểu thức tính biên độ dao động tổng hợp: ${A^2} = A_1^2 + A_2^2 + 2{A_1}{A_2}cos\Delta \varphi $

Lời giải chi tiết:

Ta có, 2 dao động vuông pha nhau

$ \Rightarrow A = \sqrt {A_1^2 + A_2^2} = \sqrt {{9^2} + {{12}^2}} = 15cm$

Chọn A

Đáp án - Lời giải

Câu hỏi 49 :

Một chất điểm tham gia đồng thời hai dao động điều hòa cùng phương, cùng tần số với các phương trình lần lượt là ${x_1} = 4cos\left( {\omega t + \dfrac{\pi }{6}} \right)cm$; ${x_2} = 3cos\left( {\omega t - \dfrac{{5\pi }}{6}} \right)cm$. Biên đọ dao động tổng hợp của vật là

A 5cm.
B 7cm.
C 3,5cm.
D 1cm.

Đáp án: D

Phương pháp giải:

Sử dụng biểu thức xác định biên độ dao động tổng hợp: ${A^2} = A_1^2 + A_2^2 + 2{A_1}{A_2}{\rm{cos}}\Delta \varphi $

Lời giải chi tiết:

Ta có độ lệch pha giữa hai dao động $\Delta \varphi = \dfrac{\pi }{6} - \left( { - \dfrac{{5\pi }}{6}} \right) = \pi $

$ \Rightarrow $ 2 dao động ngược pha nhau

$ \Rightarrow $ Biên độ dao động tổng hợp: $A = 4 - 3 = 1cm$

Chọn D

Đáp án - Lời giải

Câu hỏi 50 :

Cho hai dao động điều hòa cùng phương có phương trình lần lượt là ${x_1} = 5cos\left( {2\pi t - \dfrac{\pi }{6}} \right)cm$ và ${x_1} = 5cos\left( {2\pi t - \dfrac{\pi }{2}} \right)cm$. Dao động tổng hợp của hai dao động này có biên độ là: