50 bài tập Ôn tập chương 3: Dòng điện xoay chiều mức độ vận dụng cao
Làm đề thiCâu hỏi 1 :
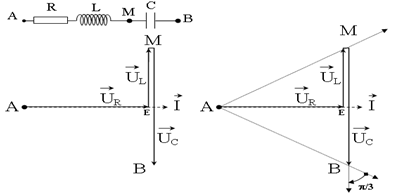
Đặt điện áp xoay chiều u = U0cosωt vào hai đầu đoạn mạch AB như hình vẽ (tụ điện có điện dung C thay đổi được). Điều chỉnh C đến giá trị C0 để điện áp hiệu dụng hai đầu tụ điện đạt cực đại, khi đó điện áp tức thời giữa A và M có giá trị cực đại là 84,5 V. Giữ nguyên giá trị C0 của tụ điện. Ở thời điểm t0, điện áp hai đầu: tụ điện, cuộn cảm thuần và điện trở có độ lớn lần lượt là 202,8 V; 30 V và uR. Giá trị uR bằng
- A 50 V.
- B 60 V.
- C 30 V.
- D 40 V.
Đáp án: C
Phương pháp giải:
Sử dụng giản đồ vecto và lí thuyết về mạch điện xoay chiều có C thay đổi để UCmax
Lời giải chi tiết:
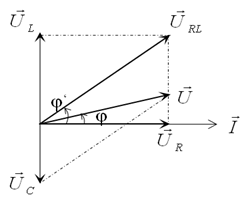
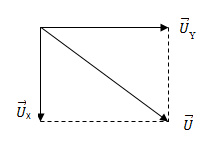
Khi C thay đổi để UCmax thì \(\overrightarrow {{U_{RL}}} \bot \overrightarrow {{U_{AB}}} \)
Ta có giản đồ vecto:
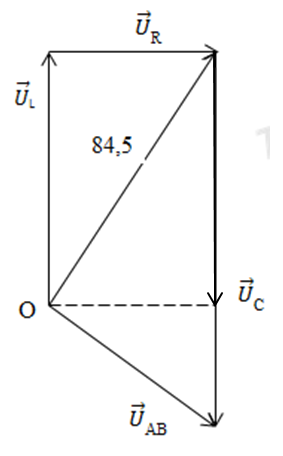
Do uC và uL ngược pha nên: \(\left| {{{{u_C}} \over {{u_L}}}} \right| = {{{U_{0C}}} \over {{U_{0L}}}} = {{202,8} \over {30}} = 6,76\)
Từ giản đồ vecto ta có: \({84,5^2} = {U_{0C}}.{U_{0L}} = 6,76.U_{0L}^2 \Rightarrow {U_{0L}} = 32,5V \Rightarrow {U_{0R}} = \sqrt {{{84,5}^2} - {{32,5}^2}} = 78V\)
Vì uL và uR vuông pha nên: \({\left( {{{{u_R}} \over {{U_{0R}}}}} \right)^2} + {\left( {{{{u_L}} \over {{U_{0L}}}}} \right)^2} = 1 \Leftrightarrow {\left( {{{{u_R}} \over {78}}} \right)^2} + {\left( {{{30} \over {32,5}}} \right)^2} = 1 \Leftrightarrow {u_R} = 30V\)
Chọn C
Câu hỏi 2 :
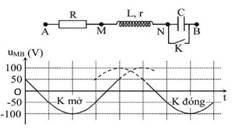
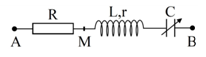
Đặt điện áp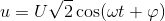 (U và ω không đổi) vào hai đầu đoạn mạch AB. Hình bên là sơ đồ mạch điện và một phần đồ thị biểu diễn sự phụ thuộc của điện áp uMB giữa hai điểm M, B theo thời gian t khi K mở và khi K đóng. Biết điện trở R = 2r. Giá trị của U là
(U và ω không đổi) vào hai đầu đoạn mạch AB. Hình bên là sơ đồ mạch điện và một phần đồ thị biểu diễn sự phụ thuộc của điện áp uMB giữa hai điểm M, B theo thời gian t khi K mở và khi K đóng. Biết điện trở R = 2r. Giá trị của U là
- A 193,2 V
- B 187,1 V.
- C 136,6 V.
- D 122,5 V.
Đáp án: D
Lời giải chi tiết:
Câu hỏi 3 :
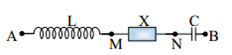
Cho dòng điện xoay chiều chạy qua đoạn mạch AB có sơ đồ như hình bên, trong đó L là cuộn cảm thuần và X là đoạn mạch xoay chiều. Khi đó, điện áp giữa hai đầu các đoạn mạch AN và MB có biểu thức lần lượt \({u_{AN}} = 30\sqrt 2 cos\omega t(V);{u_{MB}} = 40\sqrt 2 cos\left( {\omega t - {\pi \over 2}} \right)(V)\). Điện áp hiệu dụng giữa hai đầu đoạn mạch AB có giá trị nhỏ nhất là
- A 16 V.
- B 50V.
- C 32V.
- D 24V.
Đáp án: D
Phương pháp giải:
Sử dụng giản đồ vecto và hệ thức lượng trong tam giác vuông
Lời giải chi tiết:
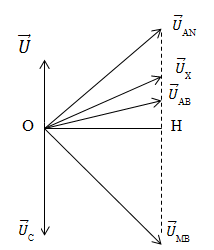
uAN = uL + uX
uMB = uC + uX
uAB = uAN + uC
UAB ≥ OH => (UAB)min = OH
Áp dụng hệ thức lượng trong tam giác vuông ta có : \({1 \over {U_{AB}^2}} = {1 \over {U_{AN}^2}} + {1 \over {U_{MB}^2}} \Rightarrow {U_{AB}} = 24V\)
Câu hỏi 4 :
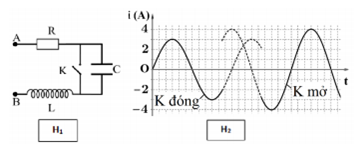
Đặt điện áp xoay chiều u = U0cos(ωt + φ) vào hai đầu đoạn mạch AB gồm điện trở R = 24 Ω, tụ điện và cuộn cảm thuần mắc nối tiếp (hình H1). Ban đầu khóa K đóng, sau đó khóa K mở. Hình H2 là đồ thị biểu diễn sự phụ thuộc của cường độ dòng điện i trong đoạn mạch vào thời gian t. Giá trị của U0 gần nhấtvới giá trị nào sau đây?
- A 170 V.
- B 212 V.
- C 127 V.
- D 255 V.
Đáp án: C
Phương pháp giải:
Sử dụng công thức I0 = U0/Z , độ lệch pha tanφ = (ZL – ZC)/R kết hợp kĩ năng đọc đồ thị
Lời giải chi tiết:
\(\eqalign{
& {{U_0^2} \over {{3^2}}} = R_0^2 + Z_L^2 \Rightarrow Z_L^2 = {{U_0^2} \over {{3^2}}} - 5,76 \cr
& {{U_0^2} \over {{4^2}}} = R_0^2 + {\left( {{Z_L} - {Z_C}} \right)^2} \Rightarrow {\left( {{Z_L} - {Z_C}} \right)^2} = {{U_0^2} \over {{4^2}}} - 5,76 \cr
& {R^2} = {Z_L}\left( {{Z_L} - {Z_C}} \right) \Rightarrow {{{R^2}} \over {Z_L^2}} = {{{Z_L} - {Z_C}} \over {{Z_L}}} \Rightarrow {{{{U_0^2} \over {{4^2}}} - 5,76} \over {{{U_0^2} \over {{3^2}}} - 5,76}} = {\left( {{{{R^2}} \over {Z_L^2}}} \right)^2} \cr} \)
\(\eqalign{
& \Rightarrow \left( {{{U_0^2} \over {{4^2}}} - 5,76} \right)\left( {{{U_0^2} \over {{3^2}}} - 5,76} \right) = {R^4}\left( {{{U_0^2} \over {{3^2}}} - 5,76} \right) \Rightarrow \left( {{{U_0^2} \over {{4^2}}} - 5,76} \right)\left( {{{U_0^2} \over {{3^2}}} - 5,76} \right) = {R^4} \cr
& \Rightarrow {{U_0^4} \over {{3^2}{{.4}^2}}} - 5,76\left( {{{U_0^2} \over {{3^2}}} + {{U_0^2} \over {{4^2}}}} \right) = 0 \Rightarrow {U_0} = R\sqrt {{3^2} + {4^2}} = 120V \cr} \)
Câu hỏi 5 :
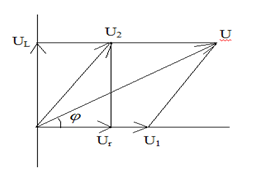
Đặt điện áp $u = 180\sqrt 2 {\text{cos}}\omega {\text{t (V)}}$ (với ω không đổi) vào hai đầu đoạn mạch AB gồm đoạn mạch AM nối tiếp đoạn mạch MB. Đoạn mạch AM có điện trở thuần R, đoạn mạch MB có cuộn cảm thuần có độ tự cảm L thay đổi được và tụ điện có điện dung C mắc nối tiếp. Điện áp hiệu dụng ở hai đầu đoạn mạch AM và độ lớn góc lệch pha của cường độ dòng điện so với điện áp u khi L = L1 là U và φ1, còn khi L = L2 thì tương ứng là $\sqrt 8 U$ và φ2. Biết ${\varphi _1} + {\varphi _2} = {90^0}$. Hệ số công suất của mạch khi L = L1 là
- A 0,33
- B 0,86
- C 0,5
- D 0,71
Đáp án: A
Lời giải chi tiết:
Ta có: Khi L = L1 thì UAM1 = UR1 = U
Khi L = L2 thì \({U_{AM2}} = \;{U_{R2}} = \sqrt 8 U\)
${\varphi _1} + {\varphi _2} = \frac{\pi }{2} \to \tan {\varphi _1}\tan {\varphi _2} = - 1 \to \frac{{{Z_{L1}} - {Z_{C1}}}}{R}.\frac{{{Z_{L1}} - {Z_{C1}}}}{R} = - 1{\text{ }}(1)$
Mặt khác: ta có
\(\eqalign{
& {{{U_{R1}}} \over {{U_{R2}}}} = {1 \over {\sqrt 8 }} \to {I_2} = \sqrt 8 {I_1} \to {Z_1} = \sqrt 8 {Z_2} \cr
& \leftrightarrow \sqrt {{R^2} + {{\left( {{Z_{L1}} - {Z_C}} \right)}^2}} = \sqrt 8 \sqrt {{R^2} + {{\left( {{Z_{L2}} - {Z_C}} \right)}^2}} \cr
& \leftrightarrow {\left( {{Z_{L1}} - {Z_C}} \right)^2} - 7{R^2} - 8{\left( {{Z_{L2}} - {Z_C}} \right)^2} = 0{\rm{ (2)}} \cr} \)
Chia cả hai vế của (2) cho (ZL2 - ZC) kết hợp với (1), Ta được:
\(\eqalign{
& {{{{\left( {{Z_{L1}} - {Z_C}} \right)}^2}} \over {{{\left( {{Z_{L2}} - {Z_C}} \right)}^2}}} - 7{{\left( {{Z_{L1}} - {Z_C}} \right)} \over {\left( {{Z_{L2}} - {Z_C}} \right)}} - 8 = 0{\rm{ }} \cr
& \to \left[ \matrix{
{{\left( {{Z_{L1}} - {Z_C}} \right)} \over {\left( {{Z_{L2}} - {Z_C}} \right)}} = 1(Loai) \hfill \cr
{{\left( {{Z_{L1}} - {Z_C}} \right)} \over {\left( {{Z_{L2}} - {Z_C}} \right)}} = - 8 \hfill \cr} \right. \cr} \)
Với \(\frac{{\left( {{Z_{L1}} - {Z_C}} \right)}}{{\left( {{Z_{L2}} - {Z_C}} \right)}} = - 8 \to - \frac{{\left( {{Z_{L1}} - {Z_C}} \right)}}{8} = \left( {{Z_{L2}} - {Z_C}} \right)\)
Thay vào (1) => \({\left( {{Z_{L1}} - {Z_C}} \right)^2} = 8{R^2}\)
Hệ số công suất của mạch khi L=L1: \({\text{cos}}{\varphi _1} = \frac{R}{{{Z_1}}} = \frac{R}{{\sqrt {{R^2} + {{\left( {{Z_{L1}} - {Z_C}} \right)}^2}} }} = \frac{R}{{3R}} = \frac{1}{3}\)
=> Chọn A
Câu hỏi 6 :
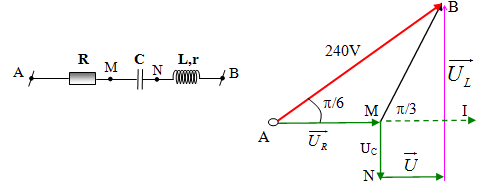
Trên đoạn mạch xoay chiều không phân nhánh có bốn điểm theo đúng thứ tự A, M, N và B. Giữa hai điểm A và M chỉ có điện trở thuần, giữa hai điểm M và N chỉ có tụ điện, giữa hai điểm N và B chỉ có cuộn cảm. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều 240V – 50 Hz thì uMB và uAM lệch pha nhau π/3, uAB vàuMB lệch pha nhau π/6. Điện áp hiệu dụng trên R là
- A 80 (V).
- B 60 (V).
- C \(80\sqrt3 V\)
- D \(60\sqrt3 V\)
Đáp án: C
Lời giải chi tiết:
Vẽ mạch điện và vẽ giản đồ véc-tơ.
Tam giác AMB cân tại M nên ta có góc ABM = p/6.
Theo ĐL hàm sin:\({{{U_R}} \over {\sin {{30}^0}}} = {U \over {\sin {{120}^0}}} \Rightarrow {U_R} = 80\sqrt 3 (V)\)
Câu hỏi 7 :
Cho đoạn mạch xoay chiều nối tiếp gồm:
Điện trở R = 60Ω; Cuộn cảm thuần có L = 0,255H;
UAB = 120V không đổi; tần số dòng điện f = 50Hz. tụ điện có điện dung C biến thiên.
Hãy xác định giá trị của C để điện áp giữa hai đầu tụ điện đạt giá trị cực đại.
- A C =15,4μF.
- B C = 20μF.
- C C =30μF.
- D C = 25,4μF.
Đáp án: D
Phương pháp giải:
Áp dụng giản đồ vecto cho mạch điện xoay chiều
Lời giải chi tiết:
Bài giải
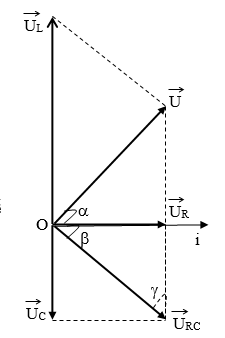
Điện áp hai đầu mạch được biểu diễn bằng véc tơ \(\vec U\) quay như hình vẽ.
\(\vec U = {\vec U_R} + {\vec U_L} + {\vec U_C}\)
gọi φ, φ’là góc lệch pha giữa \({\vec U_{RL}}\) và \(\vec U\) so với \(\vec I\).
Theo định lí hàm số sin ta có:
\({{{U_c}} \over {\sin (\varphi ' - \varphi )}} = {U \over {\sin ({\pi \over 2} - \varphi ')}}\) =>\({U_C} = {{\sin (\varphi ' - \varphi )} \over {\cos \varphi '}}.U\)
Khi C biến thiên thì φ thay đổi, UC cực đại khi sin(φ’- φ) = 1=> φ’- φ =π/2
tanφ = -cotanφ’ hay tanφ.tanφ’ = -1
=>\({{{Z_L} - {Z_C}} \over R} = - {R \over {{Z_L}}}\) =>\({Z_C} = {{{R^2} + {Z_L}^2} \over {{Z_L}}}\) = 125Ω => C = 25,4μF.
Câu hỏi 8 :
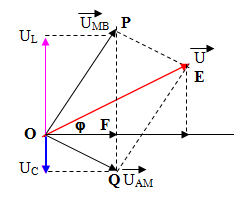
Cho mạch điện như hình vẽ. Đặt vào hai đầu đoạn mạch điện áp xoay chiều u=120\(\sqrt6\) cos(100 t)(V) ổn định, thì điện áp hiệu dụng hai đầu MB bằng 120V, công suât tiêu thụ toàn mạch bằng 360W; độ lệch pha giữa uAN và uMB là 900, uAN và uAB là 600 . Tìm R và r
- A R=120 Ω; r = 60 Ω
- B R=60 Ω ; r=30 Ω ;
- C R=60 Ω ; r=120 Ω
- D R=30 Ω ; r=60 Ω
Đáp án: B
Lời giải chi tiết:
Giải:
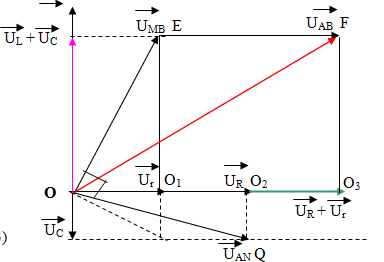
Vẽ giản đồ véc tơ như hình vẽ
\(\eqalign{
& \overrightarrow {O{O_1}} = \overrightarrow {{U_r}} \cr
& \overrightarrow {{U_R}} = \overrightarrow {O{O_2}} = \overrightarrow {{O_1}{O_2}} = \overrightarrow {EF} \cr
& \overrightarrow {{U_{MB}}} = \overrightarrow {OE} ;{U_{MB}} = 120V(1) \cr
& \overrightarrow {{U_{AN}}} = \overrightarrow {OQ} ;\overrightarrow {{U_{AB}}} = \overrightarrow {OF} = 120\sqrt 3 \left( 2 \right) \cr} \)
 EOQ = 900
EOQ = 900
FOQ = 600
Suy ra a = EOF = 900 – 600 = 300.
EOF = 900 – 600 = 300.
Xét tam giác OEF: EF2 = OE2 + OF2 – 2.OE.OFcos300
Thay số => EF = OE = 120 (V) Suy ra UR = 120(V) (3)
UAB2 = (UR + Ur)2 + (UL – UC)2
Với (UL – UC)2 = UMB2 – Ur2 ( xét tam giác vuông OO1E)
UAB2 = UR2 +2UR.Ur + UMB2 . Từ (1); (2), (3) ta được Ur = 60 (V) (4)
Góc lệch pha giữa u và i trong mạch:
φ=  FOO3 = 300 ( vì theo trên tam giác OEF là tam giác cân có góc ở đáy bằng 300)
FOO3 = 300 ( vì theo trên tam giác OEF là tam giác cân có góc ở đáy bằng 300)
Từ công thức P = UIcosφ => I = P / Uφcos 360/(120 cos300) = 2 (A): I = 2A (5)
Do đó R = UR/I = 60W; r = Ur /I = 30W. Chọn B
Câu hỏi 9 :
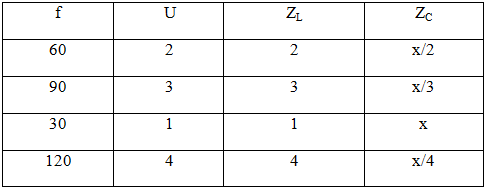
Cho mạch điện xoay chiều RLC mắc nối tiếp, cuộn dây thuần cảm. Các giá trị của điện trở R, độ tự cảm L điện dung C thỏa điều kiện 4L = CR2. Đặt vào hai đầu đoạn mạch điện áp xoay chiều ổn định, có tần số thay đổi được (với f < 125 Hz). Khi tần số f1 = 60Hz thì hệ số công suất của mạch điện là k. Khi tần số f2 =120Hz thì hệ số công suất của mạch điện là \({k_2} = {5 \over 4}k{}_1\). Khi tần số là f3 thì hệ số công suất của mạch điện là \({k_3} = {{60} \over {61}}\). Giá trị của f3 gần giá trị nào nhất sau đây?
- A 65 Hz
- B 80 Hz
- C 100 Hz
- D 110 Hz
Đáp án: C
Phương pháp giải:
Chuẩn hoá số liệu
Lời giải chi tiết:
Đây là dạng tần số thay đổi liên quan đến hệ số công suất
Giả sử f3 = n.f
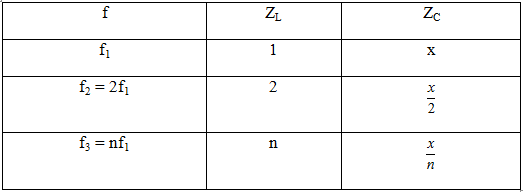
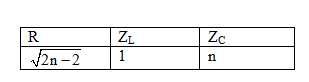
Theo bài, tỉ lệ giữa các tần số và chọn đại lượng ZL để chuẩn hóa, ta có bảng chuẩn hóa sau:
Theo đề: 4L = CR2 Þ R2 = 4ZL.ZC (1) thế vào biểu thức tổng trở:
Ta có tổng trở: \(Z = \sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} = \sqrt {4{Z_L}.{Z_C} + {{({Z_L} - {Z_C})}^2}} = \sqrt {Z_L^2 + 2{Z_L}.{Z_C} + Z_C^2} = {Z_L} + {Z_C}\)
- Theo đề: \({k_2} = {5 \over 4}{k_1}\) thì \(\cos {\varphi _2} = {5 \over 4}\cos {\varphi _1} \Leftrightarrow {R \over {{Z_2}}} = {5 \over 4}.{R \over {{Z_1}}} \Leftrightarrow {R \over {{Z_{L2}} + {Z_{C2}}}} = {5 \over 4}.{R \over {{Z_{L1}} + {Z_{C1}}}} \Leftrightarrow {R \over {2 + {x \over 2}}} = {5 \over 4}.{R \over {1 + x}}\)
\( \Rightarrow {1 \over {2 + {x \over 2}}} = {5 \over 4}.{1 \over {1 + x}} \Rightarrow x = 4;R = 4\)
-Theo đề: \({k_3} = {{60} \over {61}}\) hay: \(\cos {\varphi _3} = {R \over {{Z_3}}} = {{60} \over {61}} \Leftrightarrow {R \over {{Z_{L3}} + {Z_{C3}}}} = {{60} \over {61}} \Leftrightarrow {4 \over {n + {4 \over n}}} = {{60} \over {61}} \Leftrightarrow {n \over {{n^2} + 4}} = {{60} \over {61}}\)
\( \Rightarrow 60{n^2} - 244n + 240 = 0\) (1)
Phương trình (1) có 2 nghiệm: n1 = 5/3 => f3 = 100Hz; n2 = 12/5 => f3 = 144 Hz
Giả thiết cho f < 125Hz nên chọn giá trị f3= 100Hz
Câu hỏi 10 :
Cho đoạn mạch AB gồm hai đoạn mạch AM nt với MB. Biết đoạn AM gồm R nt với C và MB có cuộn cảm có độ tự cảm L và điện trở r. Đặt vào AB một điện áp xoay chiều u = U\(\sqrt2\) cosωt (v). Biết R = r = \(\sqrt {{L \over C}} \), điện áp hiệu dụng giữa hai đầu MB lớn gấp n =\(\sqrt3\) điện áp hai đầu AM. Hệ số công suất của đoạn mạch có giá trị là
- A 0,866
- B 0,975
- C 0,755
- D 0,887
Đáp án: A
Lời giải chi tiết:
Giải: Vẽ giản đồ véc tơ như hình vẽ
Từ R = r = \(\sqrt {{L \over C}} \) => R2 = r2 = ZL.ZC
= I2(R2 +ZC2)
= I2(r2+ ZL2) = I2(R2+ ZL2)
Xét tam giác OPQ: PQ = UL + UC
PQ2 = (UL + UC )2 = I2(ZL +ZC)2 = I2(ZL2 +ZC2 +2ZLZC) = I2 (ZL2 +ZC2 +2R2) (1)
OP2 + OQ2 = \(U_{AM}^2 + U_{MB}^2 = 2U_R^2 + U_L^2 + U_C^2 = {I^2}(2{R^2} + Z_L^2 + Z_C^2) \)(2)
Từ (1) và (2) ta thấy PQ2 = OP2 + OQ2 => tam giác OPQ vuông tại O
Từ UMB = nUAM = UAM
tan( POE) = \({{U_{AM}^{}} \over {{U_{MB}}}} = {1 \over {\sqrt 3 }}\) =>
POE) = \({{U_{AM}^{}} \over {{U_{MB}}}} = {1 \over {\sqrt 3 }}\) => 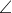 POE = 300. Tứ giác OPEQ là hình chữ nhật
POE = 300. Tứ giác OPEQ là hình chữ nhật
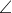 OQE = 600 ------>
OQE = 600 ------> 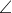 QOE = 300
QOE = 300
Do đó góc lệch pha giữa u và i trong mạch: φ = 900 – 600 = 300
Vì vậy cosφ = cos300 = \({{\sqrt 3 } \over 2} = 0,866\). Chọn A
Câu hỏi 11 :
Đặt điện áp \(u = U\sqrt 2 c{\rm{os}}2\pi ft\) (f thay đổi được, U tỉ lệ thuận với f) vào hai đầu đoạn mạch AB gồm đoạn mạch AM mắc nối tiếp với đoạn mạch MB. Đoạn mạch AM gồm điện trở thuần R mắc nối tiếp với tụ điện có điện dung C, đoạn mạch MB chỉ có cuộn cảm thuần có độ tự cảm L. Biết 2L > R2C. Khi f = 60 Hz hoặc f = 90 Hz thì cường độ dòng điện hiệu dụng trong mạch có cùng giá trị. Khi f = 30 Hz hoặc f = 120 Hz thì điện áp hiệu dụng hai đầu tụ điện có cùng giá trị. Khi f = f1 thì điện áp ở hai đầu đoạn mạch MB lệch pha một góc 1350 so với điện áp ở hai đầu đoạn mạch AM. Giá trị của f1 bằng.
- A 60 Hz
- B 80 Hz
- C 50 Hz
- D 120 Hz
Đáp án: B
Phương pháp giải:
Chuẩn hoá số liệu
Lời giải chi tiết:
*Khi f = 30Hz thì ta gán: U = 1V; ZL = 1Ω; ZC = x (Ω) ta lập bảng sau:
* Trường hợp f = 30Hz và f = 120Hz thấy UC bằng nhau nên ta có:
\({U_{C3}} = {U_{C4}} \Leftrightarrow {{{U_3}.{Z_{C3}}} \over {{Z_3}}} = {{{U_4}.{Z_{C4}}} \over {{Z_4}}} \Leftrightarrow {{1x} \over {\sqrt {{R^2} + {{(1 - x)}^2}} }} = {{4{x \over 4}} \over {\sqrt {{R^2} + {{(1 - {x \over 4})}^2}} }} \Rightarrow 1 - x = {x \over 4} - 4 \Rightarrow x = 4\)
* Trường hợp f = 60Hz và f = 90Hz ta thấy I bằng nhau nên ta có (Thế x = 4 vào)
\({I_1} = {I_2} \Leftrightarrow {{{U_1}} \over {{Z_1}}} = {{{U_2}} \over {{Z_2}}} \Leftrightarrow {2 \over {\sqrt {{R^2} + {{(2 - {x \over 2})}^2}} }} = {3 \over {\sqrt {{R^2} + {{(3 - {x \over 3})}^2}} }} \Leftrightarrow {2 \over {\sqrt {{R^2} + {{(2 - 2)}^2}} }} = {3 \over {\sqrt {{R^2} + {{(3 - {4 \over 3})}^2}} }} \Rightarrow R = {{2\sqrt 5 } \over 3}\)
* Điện áp UMB lệch 1350 với điện áp UAM, mà UMB hướng thẳng đứng lên.
Suy ra điện áp UAM hợp với trục dòng điện góc 450
Do vậy: \({Z_C} = R = {{2\sqrt 5 } \over 3} \Rightarrow {{30} \over {{f_1}}} = {{2\sqrt 5 } \over {3.4}} \Rightarrow {f_1} = 36\sqrt 5 Hz\)
Chọn B
Câu hỏi 12 :
Một cuộn cảm có độ tự cảm \(L = {{0,5.\sqrt 2 } \over \pi }(H)\) mắc nối tiếp với một điện trở thuần R. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều tần số f = 50Hz có giá trị hiệu dụng U = 100V thì điện áp hai đầu R là U1 =\(25\sqrt 2 (V)\) , hai đầu cuộn dây là U2 =\(25\sqrt {10} (V)\) . Công suất tiêu thụ của đoạn mạch là:
- A \(50\sqrt 2 (W).\)
- B \({{125\sqrt 6 } \over 4}(W).\)
- C \(25\sqrt 6 (W).\)
- D \(50\sqrt 6 (W).\)
Đáp án: A
Lời giải chi tiết:
Dễ thấy rằng cuộn dây không thuần cảm, có điện trở thuần r.
\(c{\rm{os}}\varphi {\rm{ = }}{{{U^2} + {U_1}^2 - {U_2}^2} \over {2U.{U_1}}} = {{{{100}^2} + {{(25\sqrt 2 )}^2} - {{(25\sqrt {10} )}^2}} \over {2.100.25\sqrt 2 }} = {1 \over {\sqrt 2 }}\)
\( \Rightarrow \varphi = {\pi \over 4} \Rightarrow \tan \varphi = {{{U_L}} \over {{U_r} + {U_1}}} = 1 \Rightarrow {U_r} = {U_L} - {U_1} = {U_L} - 25\sqrt 2 (1)\)Lại có \({U_r}^2 + {U_L}^2 = {U_2}^2 = {(25\sqrt {10} )^2}\) (2)
Giải (1) và (2) ta có \({U_L} = 50\sqrt 2 (V),{U_r} = 25\sqrt 2 (V)\)
\(\Rightarrow I = {{{U_L}} \over {{Z_L}}} = 1(A) \Rightarrow r = {{{U_r}} \over I} = 25\sqrt 2 (\Omega ),R = {{{U_R}} \over I} = 25\sqrt 2 (\Omega )\)
Vậy công suất tiêu thụ trên toàn mạch là P = \({I^2}(R + r) = 50\sqrt 2 ({\rm{W}})\)
Câu hỏi 13 :
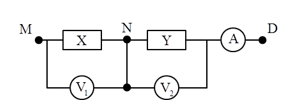
Cho mạch điện như hình vẽ: X, Y là hai hộp, mỗi hộp chỉ chứa 2 trong 3 phần tử: điện trở thuần, cuộn cảm thuần và tụ điện mắc nối tiếp. Ampe kế có điện trở rất nhỏ, các vôn kế có điện trở rất lớn. Các vôn kế và ampe kế đo được cả dòng điện xoay chiều và một chiều. Ban đầu mắc hai điểm N, D vào hai cực của một nguồn điện không đổi thì V2 chỉ 45 V, ampe kế chỉ 1,5 A. Sau đó mắc M, D vào nguồn điện xoay chiều có điện áp u = 120cos100πt V thì ampe kế chỉ 1 A, hai vôn kế chỉ cùng một giá trị và uMNlệch pha 0,5π so với uND. Khi thay tụ C trong mạch bằng tụ C’ thì số chỉ vôn kế V1 lớn nhất U1max. Giá trị UImax gần giá trị nào nhất sau đây ?
- A 90 V.
- B 75 V
- C 120 V.
- D 105 V
Đáp án: D
Lời giải chi tiết:
Đáp án D
+ Khi mắc vào hai cực ND một điện áp không đổi \( \to \) có dòng trong mạch với cường độ \(I = 1,5\,\,{\rm{A}} \to \) ND không thể chứa tụ (tụ không cho dòng không đổi đi qua) và \({{\rm{R}}_Y} = \frac{{40}}{{1,5}} = 30\,\,\Omega \).
+ Mắc vào hai đầu đoạn mạch MB một điện áp xoay chiều thì \({u_{ND}}\) sớm pha hơn \({u_{MN}}\) một góc \(0,5\pi \to \) X chứa điện trở \({{\rm{R}}_X}\) và tụ điện C, Y chứa cuộn dây L và điện trở \({{\rm{R}}_Y}\).
\( \to \) với \({V_1} = {V_2} \to {U_X} = {U_Y} = 60\,\,V \to {Z_X} = {Z_Y} = 60\,\,\Omega \)
+ Cảm kháng của cuộn dây \({{\rm{Z}}_L} = \sqrt {Z_Y^2 - R_Y^2} = \sqrt {{{60}^2} - {{30}^2}} = 30\sqrt 3 \,\,\Omega \).
+ Với \({u_{MN}}\) sớm pha \(0,5\pi \) so với \({u_{N{\rm{D}}}}\) và \(\tan {\varphi _Y} = \frac{{{Z_L}}}{{{R_Y}}} = \frac{{30\sqrt 3 }}{{30}} = \sqrt 3 \to {\varphi _Y} = 60^\circ \)
\( \to {\varphi _X} = 30^\circ \)
\( \to \left\{ \begin{array}{l}{R_X} = 30\sqrt 3 \\{Z_C} = 30\end{array} \right.\,\,\Omega \).
+ Điện áp hiệu dụng hai đầu MN:
\({V_1} = {U_{MN}} = \frac{{U\sqrt {R_X^2 + Z_C^2} }}{{\sqrt {{{\left( {{R_X} + {R_Y}} \right)}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = \frac{{60\sqrt 2 \sqrt {{{\left( {30\sqrt 3 } \right)}^2} + Z_C^2} }}{{\sqrt {{{\left( {30\sqrt 3 + 30} \right)}^2} + {{\left( {30\sqrt3 - {Z_C}} \right)}^2}} }}\)
+ Sử dụng bảng tính Mode \( \to \) 7 trên Casio ta tìm được \({V_{1\max }}\) có giá trị lân cận 105 V
Câu hỏi 14 :
Đặt điện áp xoay chiều hiệu dụng U vào hai đầu một hộp đen X thì dòng điện trong mạch có cường độ hiệu dụng là 0,25A và sớm pha π/2 so với điện áp hai đầu hộp đen X. Cũng đặt điện áp đó vào hai đầu hộp đen Y thì dòng điện trong mạch vẫn có cường độ hiệu dụng là 0,25A nhưng cùng pha với điện áp hai đầu đoạn mạch. Nếu đặt điện áp trên vào hai đầu đoạn mạch gồm X và Y mắc nối tiếp thì cường độ hiệu dụng của dòng điện trong đoạn mạch là:
- A \({{\sqrt 2 } \over 4}\)A
- B \({{\sqrt 2 } \over 8}\)A
- C \({{\sqrt 2 } \over 2}\)A
- D \(\sqrt2\)
Đáp án: B
Phương pháp giải:
Sử dụng giản đồ vecto và công thức tính cường độ dòng điện hiệu dụng I = U/Z
Lời giải chi tiết:
Đáp án B
- Đặt điện áp xoay chiều hiệu dụng U vào hai đầu một hộp đen X: \({Z_X} = \frac{U}{{0,25}} = 4U\)
- Cũng đặt điện áp đó vào hai đầu hộp đen Y: \({Z_Y} = \frac{U}{{0,25}} = 4U\)
- Đặt điện áp trên vào hai đầu đoạn mạch gồm X và Y mắc nối tiếp:
Ta có: \(Z = \sqrt {Z_X^2 + Z_Y^2} = \sqrt {{{\left( {4U} \right)}^2} + {{\left( {4U} \right)}^2}} = 4\sqrt 2 U \Rightarrow I = \frac{U}{Z} = \frac{U}{{4\sqrt 2 U}} = \frac{{\sqrt 2 }}{8}A\)
Câu hỏi 15 :
Đặt điện áp xoay chiều u = U0cosωt (U0 và ω có giá trị dương, không đổi) vào hai đầu đoạn mạch AB như hình bên, trong đó tụ điện có điện dung C thay đổi được. Biết R = 5r, cảm kháng của cuộn dây ZL = 4r và CLω2 > 1. Khi C = C0 và khi C = 0,5C0 thì điện áp giữa hai đầu M, B có biểu thức tương ứng là u1 = U01cos(ωt + φ) và u2 = U02cos(ωt + φ) (U01 và U02 có giá trị dương). Giá trị của φ là
- A 0,47 rad.
- B 0,62 rad.
- C 1,05 rad.
- D 0,79 rad.
Đáp án: D
Lời giải chi tiết:
Đáp án D
\(\varphi = {\tan ^{ - 1}}\left( {\frac{{{Z_L} - {Z_C}}}{r}} \right) - {\tan ^{ - 1}}\left( {\frac{{{Z_L} - {Z_C}}}{{R + r}}} \right)\)(1);
theo bài ta có \({\tan ^{ - 1}}\left( {\frac{{{Z_L} - {Z_C}}}{r}} \right) - {\tan ^{ - 1}}\left( {\frac{{{Z_L} - {Z_C}}}{{R + r}}} \right) = {\tan ^{ - 1}}\left( {\frac{{{Z_L} - 2{Z_C}}}{r}} \right) - {\tan ^{ - 1}}\left( {\frac{{{Z_L} - 2{Z_C}}}{{R + r}}} \right)\)
\({\tan ^{ - 1}}\left( {\frac{{4r - {Z_C}}}{r}} \right) - {\tan ^{ - 1}}\left( {\frac{{4r - {Z_C}}}{{6r}}} \right) = {\tan ^{ - 1}}\left( {\frac{{4r - 2{Z_C}}}{r}} \right) - {\tan ^{ - 1}}\left( {\frac{{4r - 2{Z_C}}}{{6r}}} \right)\)=>ZC=r; thay vào (1) ta tìm được \(\varphi = 0,785rad\)
Câu hỏi 16 :
Đặt điện áp u = U 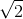 cosωt(V) (U và ω không đổi) vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở R, tụ điện có điện dung C, cuộn cảm thuần có độ tự cảm L thay đổi được. Khi L = L1 thì điện áp hiệu dụng ở hai đầu cuộn cảm có giá trị cực đại
cosωt(V) (U và ω không đổi) vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở R, tụ điện có điện dung C, cuộn cảm thuần có độ tự cảm L thay đổi được. Khi L = L1 thì điện áp hiệu dụng ở hai đầu cuộn cảm có giá trị cực đại 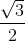 ULmax và điện áp ở hai đầu đoạn mạch sớm pha hơn dòng điện trong mạch là α ( 0 < α < π/2). Khi L = L2 điện áp hiệu dụng ở hai đầu cuộn cảm có giá trị ULmax và điện áp hai đầu đoạn mạch sơm pha so với cường độ dòng điện là 0,5 α. Tỉ số giữa điện trở và dung kháng là
ULmax và điện áp ở hai đầu đoạn mạch sớm pha hơn dòng điện trong mạch là α ( 0 < α < π/2). Khi L = L2 điện áp hiệu dụng ở hai đầu cuộn cảm có giá trị ULmax và điện áp hai đầu đoạn mạch sơm pha so với cường độ dòng điện là 0,5 α. Tỉ số giữa điện trở và dung kháng là
- A \(\sqrt 3 \)
- B \({1 \over {\sqrt 3 }}\)
- C \(\sqrt 2 \)
- D \({2 \over {\sqrt 3 }}\)
Đáp án: A
Phương pháp giải:
Áp dụng lí thuyết về bài toán điện xoay chiều có L thay đổi, sử dụng giản đồ vectơ
Lời giải chi tiết:
Ta có hình vẽ sau:
Theo giản đồ vectơ và định lý hàm số sin trong tam giác ta có : \({{{U_L}} \over {\sin (\alpha + \beta )}} = {U \over {\sin \gamma }}\)
Vì \(\sin \gamma = \cos \beta = {{{U_R}} \over {{U_{RC}}}} = {R \over {\sqrt {{R^2} + Z_C^2} }} = const\) , suy ra
\({U_L} = {U \over {\sin \gamma }}\sin (\alpha + \beta ) = {U \over {\cos \beta }}\sin (\alpha + \beta )\)
Do cos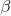 và U là các giá trị không đổi nên hiệu điện thế ULmax khi \(\sin (\alpha + \beta ) = 1 \Rightarrow \alpha + \beta = {\pi \over 2}\)
và U là các giá trị không đổi nên hiệu điện thế ULmax khi \(\sin (\alpha + \beta ) = 1 \Rightarrow \alpha + \beta = {\pi \over 2}\)
Hay nói cách khác, khi L = L1 thì ULmax => ta có uRC vuông pha với u hai đầu đoạn mạch (hình vẽ)
Từ hình vẽ ta có \({U_{L\max }} = {U \over {\sin \gamma }} = {U \over {\cos \beta }} \Rightarrow U = {U_{L\max }}\cos \beta \)
+ Khi L = L2 thì ta có độ lệch pha giữa u và i là φ thì ta có
\({{{U_L}} \over {\sin (\varphi + \beta )}} = {U \over {\sin \gamma }} \Rightarrow {U_L} = U{{\sin \left( {\varphi + \beta } \right)} \over {\sin \gamma }} = {U_{L\max }}\cos \beta {{\sin \varphi \cos \beta + \sin \beta \cos \varphi } \over {\sin \gamma }}\)
\({U_L} = {U_{L\max }}\left( {\sin \varphi \sin \alpha + \sin \beta \cos \varphi } \right)\)
Mà sinβ = cos α nên ta có \({U_L} = {U_{L\max }}\left( {\sin \varphi \sin \alpha + \cos \alpha \cos \varphi } \right) = {U_{L\max }}\cos \left( {\alpha - \varphi } \right)\)
Theo đề bài ta có \({U_L} = {{\sqrt 3 } \over 2}{U_{L\max }};\varphi = \alpha \) nên ta có
\( \Leftrightarrow {{\sqrt 3 } \over 2}{U_{L\max }} = {U_{L\max }}cos\left( {\alpha - 0,5\alpha } \right) \Rightarrow \alpha = {\pi \over 3}\)
Mà \(\sin \alpha = \cos \beta = {{{U_R}} \over {{U_{RC}}}} = {R \over {\sqrt {{R^2} + Z_C^2} }} = {{\sqrt 3 } \over 2} \Leftrightarrow 4{R^2} = 3\left( {{R^2} + Z_C^2} \right) \Rightarrow {R \over {{Z_C}}} = \sqrt 3 \)
Chọn đáp án A
Câu hỏi 17 :
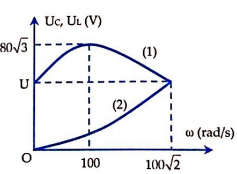
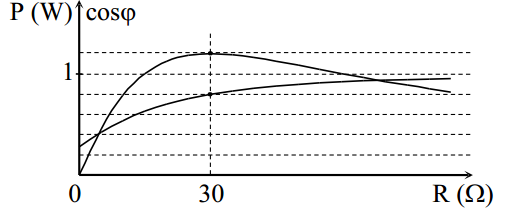
Người ta thực hiện thí nghiệm khảo sát sự phụ thuộc các điện áp hiệu dụng UL, UC của một đoạn mạch RLC mắc nối tiếp (cuộn dây thuần cảm) theo tần số góc ω (từ 0 rad/s đến 100\(\sqrt{2}\) rad/s) và vẽ được đồ thị như hình bên. Đồ thị (1) biểu thị sự phụ thuộc của UC vào ω, đồ thị (2) biểu thị sự phụ thuộc của UL và ω. Giá trị hiệu dụng của điện áp xoay chiều u đặt vào hai đầu đoạn mạch trong thí nghiệm là
- A 120V
- B 170V
- C 110V
- D 85V
Đáp án: A
Phương pháp giải:
Phương pháp chuẩn hóa số liệu
Gọi ωL; ωC là tần số góc khi ULmax và khi UCmax ta có ωC < ωL
Đặt \(n=\frac{{{\omega }_{L}}}{{{\omega }_{C}}}=\frac{1}{1-\frac{{{R}^{2}}C}{2L}};{{U}_{L\max }}={{U}_{C\max }}=\frac{2LU}{R\sqrt{4LC-{{R}^{2}}{{C}^{2}}}}\)
Chuẩn hóa:
ULmax
UCmax
Ta được
ULmax = UCmax = \(\frac{U}{\sqrt{1-{{n}^{-2}}}}\)
Lời giải chi tiết:
Áp dụng kết quả chuẩn hóa ta được
UCmax = \(\frac{U}{\sqrt{1-{{n}^{-2}}}}\)
Từ đồ thị hình vẽ ta thấy: ωC = 100 rad/s; ωL = \(100\sqrt{2}\) rad/s
Vậy \(n={{\left( \frac{{{\omega }_{L}}}{{{\omega }_{C}}} \right)}^{2}}=2\)
Nên UCmax = \(\frac{U}{\sqrt{1-{{n}^{-2}}}}=\frac{U}{\sqrt{1-{{2}^{-2}}}}=80\sqrt{3}\Rightarrow U=120V\)
Chọn A
Câu hỏi 18 :
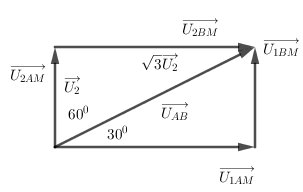
Đặt điện áp xoay chiều \(u=220\sqrt{2}\cos \left( \omega t+\varphi \right)\) vào hai đầu đoạn mạch AB như hình vẽ. Biết tụ điện có điện dung C thay đổi được. Khi C = C1 thì điện áp hiệu dụng hai đầu AM là U1, điện áp hiệu dụng hai đầu MB là U2 và cường độ dòng điện qua mạch là \({{i}_{1}}={{I}_{0}}\cos \omega t\left( A \right)\). Khi C = C2 thì điện áp hiệu dụng hai đầu MB là \(\sqrt{3}{{U}_{2}}\) và cường độ dòng điện qua đoạn mạch là \({{i}_{2}}={{I}_{02}}\cos \left( \omega t+0,5\pi \right)\left( A \right)\) . Điện áp cực đại hai đầu AM lúc đầu là
- A \(100\sqrt{6}V\)
- B \(220\sqrt{2}V\)
- C \(100\sqrt{2}V\)
- D \(100\sqrt{3}V\)
Đáp án: A
Phương pháp giải:
Áp dụng giản đồ vecto trong mạch điện xoay chiều
Lời giải chi tiết:
Từ đầu bài ta có \({{i}_{1}}\bot {{i}_{2}};{{u}_{R\left( {{C}_{1}} \right)}}\bot {{u}_{R\left( {{C}_{2}} \right)}}=>{{u}_{AM}}\bot {{u}_{MB}}\) .
Từ giản đồ vecto ta có \({{U}_{AM}}={{U}_{AB}}\cos 30=>{{U}_{AM}}=200\sqrt{2}.\frac{\sqrt{3}}{2}=100\sqrt{6}\left( V \right)\)
Chọn A
Câu hỏi 19 :
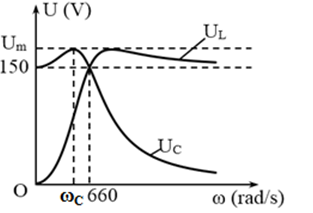
Cho mạch điện xoay chiều gồm một điện trở thuần, cuộn cảm thuần và tụ điện mắc nối tiếp theo thứ tự đó. Đặt vào hai đầu đoạn mạch điện áp xoay chiều có giá trị hiệu dụng không đổi và tân số góc ω thay đổi được. Điện áp hiệu dụng giữa hai bản tụ điện và điện áp hiệu dụng hai đầu cuộn cảm lần lượt là UC, UL phụ thuộc vào ω, chúng được biểu diễn bằng các đồ thị như hình vẽ bên, tương ứng với các đường UC, UL. Khi ω = ωC thì UC đạt cực đại là Um. Giá trị của Um là:
- A \(150\sqrt 2 V\)
- B \(100\sqrt 3 V\)
- C \(150\sqrt 3 V\)
- D \(200\sqrt 3 V\)
Đáp án: B
Phương pháp giải:
Phương pháp:
Mạch điện xoay chiều có ω thay đổi
Lời giải chi tiết:
Cách giải:
Khi \(\omega = 0 \Rightarrow \left( \begin{array}{l}{Z_C} = \infty ,{Z_L} = 0 \Rightarrow {U_L} = 0\\{Z_C} = \infty = {Z_{AB}} \Rightarrow {U_C} = {U_{AB}} = 150\end{array} \right.\)
Từ đồ thị ta có: ωR = 660 (ω để có cộng hưởng)
Tồn tại hai giá trị của ω cho cùng giá trị của UC.
Ta có:\(\left( \begin{array}{l}{\omega _1} = 0\\{\omega _2} = 660\end{array} \right. \Rightarrow \omega _C^2 = \frac{1}{2}\left( {\omega _1^2 + \omega _2^2} \right) \Rightarrow {\omega _C} = 466,7\)
Mà: \({\omega _L}{\omega _C} = \omega _R^2 \Rightarrow {\omega _L} = 933,36\)
Giá trị của Um là: \({U_m} = \frac{{{U_{AB}}}}{{\sqrt {1 - {{\left( {\frac{{{\omega _C}}}{{{\omega _L}}}} \right)}^2}} }} = 100\sqrt 3 V\)
Chọn B
Câu hỏi 20 :
Cho mạch điện xoay chiều AB theo thứ tự gồm điện trở thuần R, cuộn dây thuần cảm L, tụ điện C mắc nối tiếp. N là điểm nằm giữa cuộn dây và tụ điện. Đặt vào hai đầu đoạn mạch điện áp xoay chiều có biểu thức \(u = {U_0}\cos \omega t\,\,\left( V \right)\) (\({U_0}\) không đổi và \(\omega \) thay đổi được). Điều chỉnh \(\omega \) để điệp áp hiệu dụng trên tụ có giá trị cực đại, khi đó \({u_{AN}}\) lệch pha \(\dfrac{{2\pi }}{5}\,\,rad\) so với \({u_{AB}}\), công suất tiêu thụ của mạch khi đó là \(100\,\,W\) và hệ số công suất của đoạn mạch AN lớn hơn hệ số công suất của đoạn mạch AB. Khi điều chỉnh \(\omega \) để công suất tiêu thụ của mạch đạt cực đại và giá trị cực đại đó bằng
- A \(100\sqrt 2 \,\,W\)
- B \(100\,\,W\)
- C \(215\,\,W\)
- D \(200\sqrt 3 \,\,W\)
Đáp án: C
Phương pháp giải:
Tần số thay đổi để điện áp hiệu dụng trên tụ cực đại: \(\tan \varphi .\tan {\varphi _{RL}} = - \dfrac{1}{2}\)
Công suất tiêu thụ của mạch điện: \(P = \dfrac{{{U^2}}}{R}{\cos ^2}\varphi = {P_{\max }}.co{s^2}\varphi \)
Công thức lượng giác: \(\tan \left( {a + b} \right) = \dfrac{{\tan a + \tan b}}{{1 - \tan a.tanb}}\)
Lời giải chi tiết:
Hệ số công suất của đoạn mạch AN lớn hơn hệ số công suất của đoạn mạch AB, ta có:
\(\cos {\varphi _{RL}} > \cos \varphi \Rightarrow \left| {\tan {\varphi _{RL}}} \right| > \left| {\tan \varphi } \right| \Rightarrow {\tan ^2}\varphi > \dfrac{1}{2} \Rightarrow \left| {\tan \varphi } \right| > 0,707\)
\({u_{AN}}\) lệch pha \(\dfrac{{2\pi }}{5}\,\,rad\) so với \({u_{AB}}\), ta có:
\(\begin{array}{l}{\varphi _{RL}} = \dfrac{{2\pi }}{5} + \varphi \Rightarrow \tan {\varphi _{RL}} = \dfrac{{\tan \dfrac{{2\pi }}{5} + \tan \varphi }}{{1 - \tan \dfrac{{2\pi }}{5}.\tan \varphi }}\\\dfrac{{\tan \dfrac{{2\pi }}{5} + \tan \varphi }}{{1 - \tan \dfrac{{2\pi }}{5}.\tan \varphi }}.\tan \varphi = - \dfrac{1}{2}\\ \Rightarrow 2{\tan ^2}\varphi + \tan \dfrac{{2\pi }}{5}.\tan \varphi + 1 = 0\\ \Rightarrow \left[ \begin{array}{l}\tan \varphi = - 0,466\,\,\left( {loai} \right)\\\tan \varphi = - 1,073\,\,\left( {t/m} \right)\end{array} \right.\\ \Rightarrow {\cos ^2}\varphi = \dfrac{1}{{1 + {{\tan }^2}\varphi }} = 0,465\\ \Rightarrow {P_{\max }} = \dfrac{P}{{{{\cos }^2}\varphi }} = \dfrac{{100}}{{0,465}} = 215\,\,\left( W \right)\end{array}\)
Chọn C.
Câu hỏi 21 :
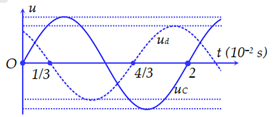
Đặt điện áp xoay chiều có giá trị hiệu dụng U = 200V vào hai đầu đoạn mạch gồm cuộn dây mắc nối tiếp với tụ điện có điện dung thay đổi. Khi đó điện áp tức thời giữa hai đầu cuộn dây và hai bản tụ biến đổi theo thời gian có đồ thị như hình vẽ. Điều chỉnh điện dung của tụ điện sao cho tổng điện áp hiệu dụng của cuộn dây và tụ điện có giá trị lớn nhất, giá trị đó bằng
- A 300\(\sqrt 2 \) V
- B 300V
- C 200\(\sqrt 3 \)V
- D 400V
Đáp án: D
Phương pháp giải:
Sử dụng giản đồ vecto và kĩ năng đọc đồ thị
Áp dụng định lí hàm số sin trong tam giác và tính chất dãy tỉ số bằng nhau
Công thức lượng giác: \(\sin a + \sin b = 2\sin {{a + b} \over 2}.\cos {{a - b} \over 2}\)
Lời giải chi tiết:
Từ đồ thị ta thấy : \(\frac{T}{2} = \left( {\frac{4}{3} - \frac{1}{3}} \right){.10^{ - 2}} \Rightarrow T = {2.10^{ - 3}}s \Rightarrow \omega = 100\pi \left( {rad/s} \right)\)
Từ đồ thị ta có phương trình của điện áp giữa hai đầu tụ điện: \(\left\{ \begin{array}{l}{u_C} = {U_{0C}}.\cos \left( {100\pi t - \frac{\pi }{2}} \right)\\{u_d} = {U_{0d}}.\cos \left( {100\pi t + \frac{\pi }{6}} \right)\end{array} \right.\)
→ ud sớm pha hơn uC một góc \(\frac{{2\pi }}{3}\) → ud sớm pha hơn ur góc \(\frac{\pi }{6}\)
Ta có giản đồ vecto:
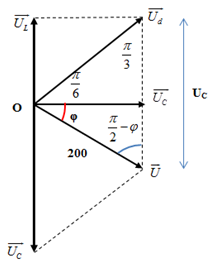
Áp dụng định lí hàm số sin trong tam giác ta có :
\(\begin{array}{l}\frac{{{U_d}}}{{\sin \left( {\frac{\pi }{2} - \varphi } \right)}} = \frac{{{U_C}}}{{\sin \left( {\frac{\pi }{6} + \varphi } \right)}} = \frac{U}{{\sin \frac{\pi }{3}}}\\ \Rightarrow \frac{{{U_d} + {U_C}}}{{\sin \left( {\frac{\pi }{2} - \varphi } \right) + \sin \left( {\frac{\pi }{6} + \varphi } \right)}} = \frac{U}{{\sin \frac{\pi }{3}}}\\ \Rightarrow {U_d} + {U_C} = \frac{U}{{\sin \frac{\pi }{3}}}.\left[ {\sin \left( {\frac{\pi }{2} - \varphi } \right) + \sin \left( {\frac{\pi }{6} + \varphi } \right)} \right]\\ \Rightarrow {\left( {{U_d} + {U_C}} \right)_{\max }} \Leftrightarrow {\left[ {\sin \left( {\frac{\pi }{2} - \varphi } \right) + \sin \left( {\frac{\pi }{6} + \varphi } \right)} \right]_{\max }}\end{array}\)
Ta có :
\(\begin{array}{l}\sin \left( {\frac{\pi }{2} - \varphi } \right) + \sin \left( {\frac{\pi }{6} + \varphi } \right) = 2.\sin \frac{\pi }{3}.\cos \frac{{2\varphi - \frac{\pi }{3}}}{2}\\ \Rightarrow {\left[ {\sin \left( {\frac{\pi }{2} - \varphi } \right) + \sin \left( {\frac{\pi }{6} + \varphi } \right)} \right]_{\max }} = 2.\sin \frac{\pi }{3}\\ \Rightarrow {\left[ {{U_d} + {U_C}} \right]_{\max }} = \frac{U}{{\sin \frac{\pi }{3}}}.2.\sin \frac{\pi }{3} = 2U = 2.200 = 400V\end{array}\)
Chọn D
Câu hỏi 22 :
Mạch điện xoau chiều AB gồm một cuộn dây có điện trở, một điện trở thuần và một tụ điện mắc nối tiếp theo thứ tự đã nêu. Điểm M ở giữa cuộn dây và điện trở thuần. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều có tần số không đổi và giá trị hiệu dụng 200V thì trong mạch có cộng hưởng điện. Lúc đó điện áp hiệu dụng trên đoạn AM là 160V, độ lệch pha giữa điện áp hai đầu AM so với cường độ dòng điện trong mạch gấp đôi độ lệch pha giữa cường độ dòng điện so với điện áp hai đầu MB. Điện áp hiệu dụng hai đầu MB là
- A 240V
- B 120V
- C 180V
- D 220V
Đáp án: A
Phương pháp giải:
Phương pháp:
Sử dụng giản đồ vecto và định lí hàm số sin trong tam giác
Lời giải chi tiết:
Cách giải:
Từ các dữ kiện bài cho ta có giản đồ vecto như hình vẽ:
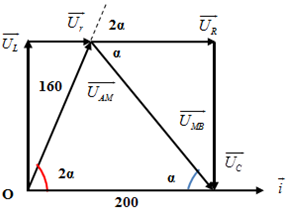
Áp dụng định lí hàm số sin trong tam giác ta có:\(\frac{{160}}{{\sin \alpha }} = \frac{{200}}{{\sin \left( {\pi {\rm{\;}} - 3\alpha } \right)}} = \frac{{{U_{MB}}}}{{\sin 2\alpha }}\)
Giải phương trình: \(\frac{{160}}{{\sin \alpha }} = \frac{{200}}{{\sin \left( {\pi {\rm{\;}} - 3\alpha } \right)}} \Rightarrow \alpha {\rm{\;}} = 5,56 \Rightarrow {U_{MB}} = 240V\)
Chọn A
Câu hỏi 23 :
Trong giờ thực hành vật lí có sử dụng bộ thí nghiệm điện xoay chiều Vật lí 12 để tiến hành lắp mạch điện. Bảng lắp ráp mạch điện được vẽ lại như hình vẽ, với các chốt cắm có tên tương ứng. Một học sinh lắp mạch như sau: giữa E, C lắp cuộn cảm thuần có độ tự cảm 31,85 mH; giữa D, K lắp một điện trở \(\text{R = 10 }\!\!\Omega\!\!\text{ }\); giữa J, I lắp một tụ xoay; giữa N, F lắp Vôn kế V1; giữa F, M lắp Vôn kế V2; giữa A, B duy trì một điện áp xoay chiều (12 V – 50 Hz). Điều chỉnh góc xoay giữa hai bản tụ điện, quan sát đồng thời số chỉ của cả hai Vôn kế. Khi tổng số chỉ của hai Vôn kế đạt giá trị lớn nhất thì công suất của mạch lúc đó là
- A 15,8 W
- B 13,8 W
- C 10,3 W
- D 12,3 W
Đáp án: D
Phương pháp giải:
Số chỉ của vôn kế V1 là điện áp hiệu dụng của ULR, số chỉ của vôn kế V2 là điện áp hiệu dụng của UC.
Lời giải chi tiết:
Ta có: Mạch điện gồm L, R, C mắc nối tiếp, tụ C thay đổi.
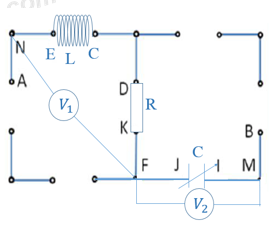
\(R=10(\Omega );{{Z}_{L}}=10(\Omega )\Rightarrow {{Z}_{L}}=R\)
\({{U}_{LR}}=\frac{{{U}_{AB}}}{Z}.{{Z}_{RL}}=\frac{{{U}_{AB}}}{\sqrt{{{R}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}}.\sqrt{{{R}^{2}}+Z_{L}^{2}}\)
\({{U}_{C}}=\frac{{{U}_{AB}}{{Z}_{C}}}{\sqrt{{{R}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}}\)
Tổng số chỉ của 2 vôn kế là:
\(U'=\frac{{{U}_{AB}}}{\sqrt{{{R}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}}.\sqrt{{{R}^{2}}+Z_{L}^{2}}+\frac{{{U}_{AB}}{{Z}_{C}}}{\sqrt{{{R}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}}=\frac{{{U}_{AB}}\left( \sqrt{2{{R}^{2}}}+{{Z}_{C}} \right)}{\sqrt{{{R}^{2}}+{{(R-{{Z}_{C}})}^{2}}}}=\frac{{{U}_{AB}}\left( \frac{\sqrt{2}R}{{{Z}_{C}}}+1 \right)}{\sqrt{\frac{2{{R}^{2}}}{Z_{C}^{2}}-2\frac{R}{{{Z}_{C}}}+1}}\)
Đặt \(\frac{\sqrt{2}R}{{{Z}_{C}}}+1=a\)\(\Rightarrow U'=\frac{{{U}_{AB}}.a}{\sqrt{{{a}^{2}}-(\sqrt{2}+2)a+\sqrt{2}+2}}=\frac{{{U}_{AB}}}{\sqrt{1-\frac{\sqrt{2}+2}{a}+\frac{\sqrt{2}+2}{{{a}^{2}}}}}\)
U’ max \(\Leftrightarrow \frac{1}{a}=\frac{2+\sqrt{2}}{2(2+\sqrt{2})}=\frac{1}{2}\Rightarrow a=2\Rightarrow \frac{\sqrt{2}R}{{{Z}_{C}}}+1=2\Rightarrow {{Z}_{C}}=\sqrt{2}R=10\sqrt{2}(\Omega )\)
Công suất của mạch lúc đó là:
\(P=\frac{{{U}^{2}}}{R}\text{co}{{\text{s}}^{2}}\varphi =\frac{{{12}^{2}}}{10}{{\left( \frac{10}{\sqrt{{{10}^{2}}+{{(10-10\sqrt{2})}^{2}}}} \right)}^{2}}=12,3(\text{W})\)
Chọn D
Câu hỏi 24 :
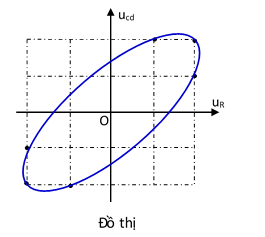
Đặt điện áp xoay chiều vào hai đầu đoạn mạch gồm điện trở R và cuộn dây có điện trở mắc nối tiếp. Hình bên là đường cong biểu diễn mối liên hệ của điện áp tức thời giữa hai đầu cuộn dây \(\left( {{u}_{cd}} \right)\) và điện áp tức thời giữa hai đầu điện trở R \(\left( {{u}_{R}} \right)\). Độ lệch pha giữa \(\left( {{u}_{cd}} \right)\) và \(\left( {{u}_{R}} \right)\) có giá trị là
- A
0,58 rad.
- B
0,93 rad
- C
1,19 rad.
- D
0,72 rad.
Đáp án: D
Phương pháp giải:
Gọi \(\alpha \) là độ lệch pha giữa điện áp hai đầu cuộn dây và hai đầu tụ điện. Áp dụng hệ thức độc lập với thời gian cho đoạn mạch chứa tụ và dây ta có:
\(\frac{u_{d}^{2}}{U_{0d}^{2}}+\frac{u_{C}^{2}}{U_{0C}^{2}}-2\frac{{{u}_{d}}}{{{U}_{0d}}}.\frac{{{u}_{C}}}{{{U}_{0C}}}.\cos \alpha =hs\)
Lời giải chi tiết:
Gọi \(\alpha \) là độ lệch pha giữa điện áp hai đầu cuộn dây và hai đầu điện trở. Áp dụng hệ thức độc lập với thời gian cho đoạn mạch chứa điện trở và cuộn dây ta có:
\(\frac{u_{d}^{2}}{U_{0d}^{2}}+\frac{u_{R}^{2}}{U_{0R}^{2}}-2\frac{{{u}_{d}}}{{{U}_{0d}}}.\frac{{{u}_{R}}}{{{U}_{0R}}}.\cos \alpha =hs\)
Nhìn vào đồ thị ta thấy có ba trường hợp đặc biệt được đánh dấu với tọa độ lần lượt là (1; 2); (2; 2); (2, 1) trên elip. Thay vào phương trình trên ta thu được:
\(\frac{4}{U_{0d}^{2}}+\frac{1}{U_{0R}^{2}}-2\frac{2}{{{U}_{0d}}}.\frac{1}{{{U}_{0R}}}.\cos \alpha =\frac{4}{U_{0d}^{2}}+\frac{4}{U_{0R}^{2}}-2\frac{2}{{{U}_{0d}}}.\frac{2}{{{U}_{0R}}}.\cos \alpha \)
Và \(\frac{1}{U_{0d}^{2}}+\frac{4}{U_{0R}^{2}}-2\frac{1}{{{U}_{0d}}}.\frac{2}{{{U}_{0R}}}.\cos \alpha =\frac{4}{U_{0d}^{2}}+\frac{4}{U_{0R}^{2}}-2\frac{2}{{{U}_{0d}}}.\frac{2}{{{U}_{0R}}}.\cos \alpha \)
Suy ra:
\(\frac{3}{U_{0R}^{2}}=\frac{4}{{{U}_{0d}}{{U}_{0R}}}.\cos \alpha \) và \(\frac{3}{U_{0d}^{2}}=\frac{4}{{{U}_{0d}}{{U}_{0R}}}.\cos \alpha \)
\(\Leftrightarrow \) \({{U}_{0d}}={{U}_{0C}}\) và \(\cos \alpha =\frac{3}{4}\)\(\Leftrightarrow \alpha =0,72\left( rad \right)\)
Chọn D
Câu hỏi 25 :
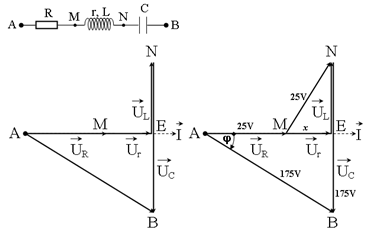
Trên đoạn mạch xoay chiều không phân nhánh có bốn điểm theo đúng thứ tự A, M, N và B. Giữa hai điểm A và M chỉ có điện trở thuần, giữa hai điểm M và N chỉ có cuộn dây, giữa 2 điểm N và B chỉ có tụ điện. Đặt vào hai đầu đoạn mạch một điện áp 175 V – 50 Hz thì điện áp hiệu dụng trên đoạn AM là 25 (V), trên đoạn MN là 25 (V) và trên đoạn NB là 175 (V). Hệ số công suất của toàn mạch là
- A 7/25.
- B 1/25.
- C 7/25.
- D 1/7.
Đáp án: C
Lời giải chi tiết:
\(\left\{ \matrix{
\Delta MNE:NE = \sqrt {{{25}^2} - {x^2}} \Rightarrow EB = 60 - \sqrt {{{25}^2} - {x^2}} \hfill \cr
\Delta AEB:A{B^2} = A{E^2} + E{B^2} \Rightarrow 30625 = {\left( {25 + x} \right)^2} + {\left( {175 - \sqrt {{{25}^2} - {x^2}} } \right)^2} \hfill \cr
\Rightarrow x = 24 \Rightarrow \cos \varphi = {{AE} \over {AB}} = {7 \over {25}} \hfill \cr} \right.\)
Chọn C
Câu hỏi 26 :
Cho mạch điện xoay chiều RLC mắc nối tiếp, cuộn dây thuần cảm. Các giá trị điện trở R, độ tự cảm L và điện dung C của tụ điện thoả mãn điều kiện 3L = CR2. Đặt vào hai đầu đoạn mạch điện áp xoay chiều ổn định, tần số của dòng điện thay đổi được. Khi tần số của dòng điện là f1 = 50Hz thì hệ số công suất của mạch điện là k1. Khi tần số f2 = 150Hz thì hệ số công suất của mạch điện là \({k_2} = \frac{5}{3}{k_1}\). Khi tần số f3 = 200Hz thì hệ số công suất của mạch là k3. Giá trị của k3 gần với giá trị nào nhất sau đây:
- A 0,45
- B 0,56
- C 0,9
- D 0,67
Đáp án: C
Phương pháp giải:
Phương pháp:
Hệ số công suất: \(\cos \varphi = \frac{R}{Z} = \frac{R}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\)
Sử dụng phương pháp chuẩn hoá số liệu
Lời giải chi tiết:
Cách giải:
Ta có: \(3L\; = C{R^2} \Rightarrow \frac{{3\omega L}}{{\omega C}} = {R^2} \Rightarrow {R^2} = 3{Z_L}.{Z_C}\)
Hệ số công suất: \(\cos \varphi = \frac{R}{Z} = \frac{R}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\)
Dùng phương pháp chuẩn hoá số liệu ta có:
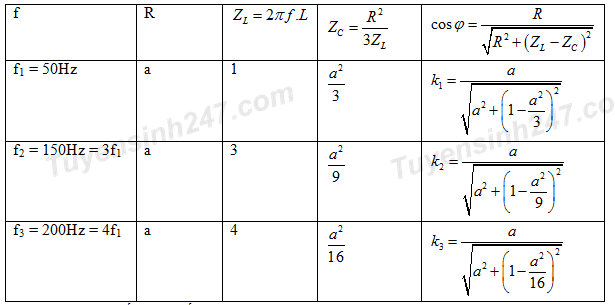
Theo bài ra ta có hệ số công suất của mạch điện là:
\(\begin{array}{l}{k_2} = \frac{5}{3}{k_1} \Leftrightarrow \frac{a}{{\sqrt {{a^2} + {{\left( {1 - \frac{{{a^2}}}{9}} \right)}^2}} }} = \frac{5}{3}.\frac{a}{{\sqrt {{a^2} + {{\left( {1 - \frac{{{a^2}}}{3}} \right)}^2}} }}\\ \Leftrightarrow 9.\left( {{a^2} + {{\left( {1 - \frac{{{a^2}}}{3}} \right)}^2}} \right) = 25.\left( {{a^2} + {{\left( {1 - \frac{{{a^2}}}{9}} \right)}^2}} \right)\\ \Leftrightarrow 9{a^2} + 9\left( {1 - \frac{2}{3}{a^2} + \frac{{{a^4}}}{9}} \right) = 25{a^2} + 25\left( {1 - \frac{2}{9}{a^2} + \frac{{{a^4}}}{{81}}} \right)\\ \Leftrightarrow \frac{{56}}{{81}}{a^4} - \frac{{148}}{9}{a^2} - 16 = 0 \Rightarrow {a^2} = 24,7218 \Rightarrow a \approx 5\end{array}\)
→ Giá trị của k3 là: \({k_3} = \frac{a}{{\sqrt {{a^2} + {{\left( {1 - \frac{{{a^2}}}{{16}}} \right)}^2}} }} = \frac{5}{{\sqrt {{5^2} + {{\left( {1 - \frac{{{5^2}}}{{16}}} \right)}^2}} }} = \frac{5}{{5,032}} = 0,9936\)
Chọn C
Câu hỏi 27 :
Đặt điện áp xoay chiều \(u = {U_0}\cos \omega t\,\,\left( V \right)\) (\({U_0}\) không đổi và \(\omega \) thay đổi được) vào hai đầu đoạn mạch gồm điện trở thuần \(R = 20\sqrt 2 \,\,\Omega \), cuộn cảm thuần có độ tự cảm \(L = \dfrac{4}{{5\pi }}\,\,H\) và tụ điện có điện dung \(C = \dfrac{{{{10}^{ - 3}}}}{{2\pi }}\,\,F\) mắc nối tiếp. Khi \(\omega = {\omega _1}\) thì \({U_{L\max }}\); \(\omega = {\omega _2}\) thì \({U_{C\max }}\). Khi \(\omega = {\omega _1} + {\omega _2}\) thì hệ số công suất của mạch bằng
- A 0,42
- B 0,58
- C 0,08
- D 0,057
Đáp án: A
Phương pháp giải:
Tần số của mạch khi có cộng hưởng: \({\omega _0} = \dfrac{1}{{\sqrt {LC} }}\)
Điện áp hiệu dụng giữa hai đầu cuộn cảm đạt cực đại khi: \({\omega _L} = {\omega _0}.\sqrt n \) với \({n^{ - 1}} = 1 - \dfrac{{C{R^2}}}{{2L}}\)
Điện áp hiệu dụng giữa hai đầu tụ điện đạt cực đại khi: \({\omega _C} = \dfrac{{{\omega _0}}}{{\sqrt n }}\)
Hệ số công suất của mạch: \(\cos \varphi = \dfrac{R}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\)
Lời giải chi tiết:
Tần số của mạch khi có cộng hưởng là:
\({\omega _0} = \dfrac{1}{{\sqrt {LC} }} = \dfrac{1}{{\sqrt {\dfrac{4}{{5\pi }}.\dfrac{{{{10}^{ - 3}}}}{{2\pi }}} }} = 50\pi \,\,\left( {rad/s} \right)\)
Ta có: \({n^{ - 1}} = 1 - \dfrac{{C{R^2}}}{{2L}} = 1 - \dfrac{{\dfrac{{{{10}^{ - 3}}}}{{2\pi }}.{{\left( {20\sqrt 2 } \right)}^2}}}{{2.\dfrac{4}{{5\pi }}}} = \dfrac{3}{4} \Rightarrow n = \dfrac{4}{3}\)
Điện áp hiệu dụng giữa hai đầu cuộn cảm đạt cực đại khi:
\({\omega _L} = {\omega _0}.\sqrt n = 50\pi .\dfrac{2}{{\sqrt 3 }} = \dfrac{{100\pi }}{{\sqrt 3 }}\,\,\left( {rad/s} \right)\)
Điện áp hiệu dụng giữa hai đầu tụ điện đạt cực đại khi:
\(\begin{array}{l}{\omega _C} = \dfrac{{{\omega _0}}}{{\sqrt n }} = \dfrac{{50\pi }}{{\dfrac{2}{{\sqrt 3 }}}} = \dfrac{{75\pi }}{{\sqrt 3 }}\,\,\left( {rad/s} \right)\\ \Rightarrow \omega = {\omega _L} + {\omega _C} = \dfrac{{100\pi }}{{\sqrt 3 }} + \dfrac{{75\pi }}{{\sqrt 3 }} = \dfrac{{175\pi }}{{\sqrt 3 }}\,\,\left( {rad/s} \right)\end{array}\)
Hệ số công suất của mạch:
\(\cos \varphi = \dfrac{R}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = \dfrac{R}{{\sqrt {{R^2} + {{\left( {\omega L - \dfrac{1}{{\omega C}}} \right)}^2}} }} = 0,42\)
Chọn A.
Câu hỏi 28 :
Đặt vào hai đầu AB điện áp xoay chiều \(u = U\sqrt 2 \cos 2\pi ft\,\,\left( V \right)\) vào hai đầu đoạn mạch AB theo thứ tự điện trở thuần, cuộn dây thuần cảm, tụ điện C mắc nối tiếp. N là điểm giữa cuộn dây và tụ điện. Điều chỉnh \(\omega \) để điện áp hiệu dụng trên tụ có giá trị cực đại, khi đó \({u_{AN}}\) lệch pha \(1,2373\,\,rad\) so với \({u_{AB}}\), công suất tiêu thụ khi đó là \(300\,\,W\). Khi điều chỉnh \(\omega \) để công suất tiêu thụ của mạch đạt giá trị cực đại thì giá trị đó bằng
- A \(300\,\,W\)
- B \(4500\,\,W\)
- C \(250\,\,W\)
- D \(525\,\,W\)
Đáp án: D
Phương pháp giải:
Tần số thay đổi để điện áp hiệu dụng trên tụ cực đại: \(\tan \varphi .\tan {\varphi _{RL}} = - \dfrac{1}{2}\)
Công suất tiêu thụ của mạch điện: \(P = \dfrac{{{U^2}}}{R}{\cos ^2}\varphi = {P_{\max }}.co{s^2}\varphi \)
Công thức lượng giác: \(\tan \left( {a + b} \right) = \dfrac{{\tan a + \tan b}}{{1 - \tan a.tanb}};co{s^2}a = \dfrac{1}{{1 + {{\tan }^2}a}}\)
Lời giải chi tiết:
\({u_{AN}}\) lệch pha \(1,2373\,\,rad\) so với \({u_{AB}}\), ta có:
\(\begin{array}{l}{\varphi _{RL}} = 1,2373 + \varphi \Rightarrow \tan {\varphi _{RL}} = \dfrac{{\tan 1,2373 + \tan \varphi }}{{1 - \tan 1,2373.\tan \varphi }}\\\dfrac{{\tan 1,2373 + \tan \varphi }}{{1 - \tan 1,2373.\tan \varphi }}.\tan \varphi = - \dfrac{1}{2}\\ \Rightarrow 2{\tan ^2}\varphi + \tan 1,2373.\tan \varphi + 1 = 0\\ \Rightarrow \left[ \begin{array}{l}\tan \varphi = - 0,5776 \Rightarrow {\cos ^2}\varphi = 0,7498\\\tan \varphi = - 0,8657 \Rightarrow {\cos ^2}\varphi = 0,5716\end{array} \right.\\ \Rightarrow \left[ \begin{array}{l}{P_{\max }} = \dfrac{P}{{{{\cos }^2}\varphi }} = \dfrac{{300}}{{0,7498}} = 400\,\,\left( W \right)\\{P_{\max }} = \dfrac{P}{{{{\cos }^2}\varphi }} = \dfrac{{300}}{{0,5716}} = 525\,\,\left( W \right)\end{array} \right.\end{array}\)
Chọn D.
Câu hỏi 29 :
Đặt điện áp xoay chiều \(U = {U_0}\cos \omega t\,\,\left( V \right)\) (\({U_0}\) không đổi và \(\omega \) thay đổi được) vào hai đầu đoạn mạch RLC mắc nối tiếp. Khi \(f = {f_1}\) thì mạch có cảm kháng là \(36\,\,\Omega \) và dung kháng là \(144\,\,\Omega \). Khi \(f = {f_2} = 120\,\,Hz\) thì cường độ dòng điện cùng pha với điện áp hai đầu đoạn mạch. Giá trị của tần số \({f_1}\) là
- A 50 Hz
- B 60 Hz
- C 85 Hz
- D 100 Hz
Đáp án: B
Phương pháp giải:
Cường độ dòng điện trong mạch cùng pha với điện áp hai đầu đoạn mạch khi: \({\omega _0} = \dfrac{1}{{\sqrt {LC} }}\)
Lời giải chi tiết:
Cường độ dòng điện trong mạch cùng pha với điện áp hai đầu đoạn mạch khi: \({\omega _0} = \dfrac{1}{{\sqrt {LC} }}\)
Khi \(f = {f_1}\), cảm kháng và dung kháng của mạch là:
\(\begin{array}{l}\left\{ \begin{array}{l}{Z_L} = {\omega _1}L = 36\,\,\left( \Omega \right)\\{Z_C} = \dfrac{1}{{{\omega _1}C}} = 144\,\,\left( \Omega \right)\end{array} \right. \Rightarrow \dfrac{{{Z_L}}}{{{Z_C}}} = \dfrac{1}{4} = {\omega _1}^2.LC \Rightarrow \dfrac{{{\omega _1}^2}}{{{\omega _0}^2}} = \dfrac{1}{4}\\ \Rightarrow \dfrac{{{\omega _1}}}{{{\omega _0}}} = \dfrac{{{f_1}}}{{{f_2}}} = \dfrac{1}{2} \Rightarrow {f_1} = \dfrac{1}{2}{f_2} = \dfrac{1}{2}.120 = 60\,\,\left( {Hz} \right)\end{array}\)
Chọn B.
Câu hỏi 30 :
Đoạn mạch nối tiếp gồm cuộn cảm thuần, đoạn mạch X và tụ điện (hình vẽ).
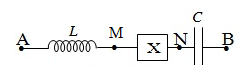
Khi đặt vào hai đầu A, B điện áp \({u_{AB}} = {U_O}cos\left( {\omega t + \varphi {\rm{\;}}} \right)\) (V); \(Uo,\omega \) và không đổi thì: \(LC{\omega ^2} = 1\), \({U_{AN}} = 30\sqrt 2 V\) và \({U_{MB}} = 60\sqrt 2 V\), đồng thời UMB trễ pha so với UAN . Nếu cảm kháng của cuộn dây là 15W thì công suất của đoạn mạch A, B có giá trị gần đúng nhất là
- A 79 W
- B 104 W
- C 60 W
- D 112W
Đáp án: B
Phương pháp giải:
Phương pháp:
Sử dụng giản đồ vecto
Sử dụng các định lí hàm số sin, hàm số cos:
\(\begin{array}{*{20}{l}}{{c^2} = {a^2} + {b^2} - 2ab.cos\varphi }\\{\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}}}\end{array}\)
Công suất của mạch: \(P = UI\cos \varphi \)
Lời giải chi tiết:
Cách giải:
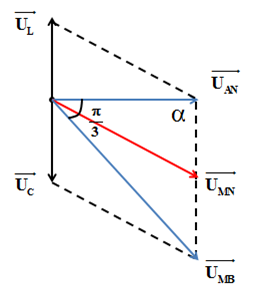
Áp dụng định lý hàm số cos: \(\frac{{{U_L} + {U_C}}}{{\sin \frac{\pi }{3}}} = \frac{{{U_{MB}}}}{{\sin \alpha }} \Rightarrow \sin \alpha {\rm{\;}} = \frac{{60\sqrt 2 .\sin \frac{\pi }{3}}}{{30\sqrt 6 }} = 1 \Rightarrow \alpha {\rm{\;}} = {90^o}\)
Lại có \(LC{\omega ^2} = 1\)\( \Rightarrow {U_L} = {U_C} = 15\sqrt 6 (V)\)
Dòng điện trong mạch: \(I = \frac{{{U_L}}}{{{Z_L}}} = \frac{{15\sqrt 6 }}{{15}} = \sqrt 6 \) (A)
Áp dụng định lý hàm số sin:\(\frac{{{U_L} + {U_C}}}{{\sin \frac{\pi }{3}}} = \frac{{{U_{MB}}}}{{\sin \alpha }} \Rightarrow \sin \alpha = \frac{{60\sqrt 2 .\sin \frac{\pi }{3}}}{{30\sqrt 6 }} = 1 \Rightarrow \alpha = {90^o}\) :
\( \Rightarrow {U_{MN}} = \sqrt {U_{AN}^2 + U_L^2} = 15\sqrt {14} \) (V)
Vì \({U_L} = {U_C} \to {U_{AB}} = {U_{MN}}\), \({\rm{cos}}\varphi {\rm{ = }}\frac{{{U_{AN}}}}{{{U_{MN}}}} = \frac{{2\sqrt 7 }}{7}\)
Công suất của mạch: \(P = UI\cos \varphi = 60\sqrt 3 \approx 104\) (W)
Chọn B
Câu hỏi 31 :
Đoạn mạch xoay chiều nối tiếp AB gồm ba đoạn AM, MN và NB. Đoạn AM chứa cuộn cảm thuần có độ tự cảm L, đoạn mạch MN chứa hộp kín X (X chỉ gồm các phần tử như điện trở thuần, cuộn cảm và tụ điện ghép nối tiếp) và đoạn NB chỉ chứa tụ điện có điện dung C. Biết điện áp uAB = U0cos(ωt + φ) (V), uAN = 80\(\sqrt 2 \)cosωt (V) và uMB = 90\(\sqrt 2 \)cos(ωt –\(\frac{\pi }{4}\) ) (V). Nếu 2LCω2 = 3 thì điện áp hiệu dụng trên đoạn MN gần nhất với giá trị nào sau đây?
- A 75V
- B 80V
- C 70V
- D 90V
Đáp án: B
Phương pháp giải:
Phương pháp:
Sử dụng giản đồ vecto
Sử dụng các định lí hàm số sin, hàm số cos:
\(\begin{array}{*{20}{l}}{{c^2} = {a^2} + {b^2} - 2ab.cos\varphi }\\{\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}}}\end{array}\)
Lời giải chi tiết:
Cách giải:
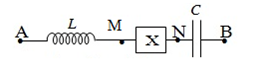
Biểu diễn các điện áp trên giản đồ vecto
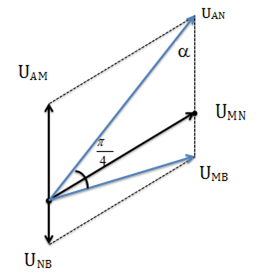
Áp dụng định lý hàm số cos:
\(\begin{array}{*{20}{l}}{{{({U_L} + {U_C})}^2} = U_{AN}^2 + U_{MB}^2 - 2.{U_{AN}}.{U_{MB}}.cos\frac{\pi }{4}}\\{ \Rightarrow {U_L} + {U_C} = \sqrt {{{(80)}^2} + {{(90)}^2} - 2.80.90.\frac{{\sqrt 2 }}{2}} = 65,7(V)}\end{array}\)
Lại có \({U_L} = I.{Z_L} = I.\omega L;{\rm{ }}{U_C} = {\rm{ }}I.{Z_C} = {\rm{ }}I.\frac{1}{{\omega C}} \Rightarrow \frac{{{U_L}}}{{{U_C}}} = {\omega ^2}LC = \frac{3}{2}\)\( \Rightarrow {U_L} = 39,4(V);{U_C} = 26,3(V)\)
Áp dụng định lý hàm số sin:\(\frac{{{U_L} + {U_C}}}{{\sin \frac{\pi }{4}}} = \frac{{{U_{MB}}}}{{\sin \alpha }} \Rightarrow \sin \alpha = \frac{{90.\sin \frac{\pi }{4}}}{{65,7}} = 0,97 \Rightarrow cos\alpha = 0,24\)
Áp dụng định lý hàm số cos:\({U_{MN}}^2 = U_{AN}^2 + U_L^2 - 2.{U_{AN}}.{U_L}{\rm{cos}}\alpha \)
\( \Rightarrow {U_{MN}} = \sqrt {{{(80)}^2} + 39,{4^2} - 2.80.39,4.0,24} = 80,2\) (V)
Chọn B
Câu hỏi 32 :
Đặt điện áp \(u = 100\sqrt 2 \cos 2\pi ft\,\,\left( V \right)\) vào hai đầu đoạn mạch RLC nối tiếp, trong đó cuộn dây thuần cảm và \(\omega \) thay đổi được. Khi \(\omega = {\omega _1} = \sqrt {45} \,\,rad/s\) thì công suất tiêu thụ của mạch là lớn nhất. Khi tần số góc \({\omega _2}\) hoặc \({\omega _3}\) thì điện áp hiệu dụng hai đầu cuộn cảm bằng nhau là \(\dfrac{{500}}{{\sqrt 7 }}\,\,V\), biết \({\omega _2}^2 + 4{\omega _3}^2 = 225\). Khi \(\omega = {\omega _4}\) thì \({U_{L\max }}\). Giá trị của \({\omega _4}^2\) là
- A \(50\,\,rad/s\)
- B \(60\,\,rad/s\)
- C \(70\,\,rad/s\)
- D \(80\,\,rad/s\)
Đáp án: A
Phương pháp giải:
Công suất tiêu thụ trong mạch lớn nhất khi mạch có cộng hưởng: \({\omega _1} = \dfrac{1}{{\sqrt {LC} }}\)
Điện áp hiệu dụng giữa hai đầu cuộn cảm: \({U_L} = \dfrac{{U.{Z_L}}}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\)
Định lí Vi – et cho phương trình bậc 2 \(a{x^2} + bx + c = 0:{x_1}{x_2} = \dfrac{c}{a}\)
Tần số để điện áp hiệu dụng hai đầu cuộn cảm đạt cực đại: \(\dfrac{2}{{{\omega _4}^2}} = \dfrac{1}{{{\omega _2}^2}} + \dfrac{1}{{{\omega _3}^2}}\)
Lời giải chi tiết:
Tần số để mạch có công suất tiêu thụ lớn nhất là: \({\omega _1} = \dfrac{1}{{\sqrt {LC} }} = \sqrt {45} \,\,\left( {rad/s} \right)\)
Điện áp hiệu dụng giữa hai đầu cuộn cảm là:
\(\begin{array}{l}{U_L} = \dfrac{{U.{Z_L}}}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} \Rightarrow \dfrac{{500}}{{\sqrt 7 }} = \dfrac{{100.{Z_L}}}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\\ \Rightarrow \dfrac{{25}}{7} = \dfrac{{{Z_L}^2}}{{{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}} \Rightarrow 25{R^2} + 25{\left( {{Z_L} - {Z_C}} \right)^2} = 7{Z_L}^2\\ \Rightarrow 18{Z_L}^2 + 25{R^2} + 25{Z_C}^2 - 50{Z_L}{Z_C} = 0\\ \Rightarrow 18{\omega ^2}{L^2} + 25{R^2} + \dfrac{{25}}{{{\omega ^2}{C^2}}} - \dfrac{{50L}}{C} = 0\\ \Rightarrow 18{\omega ^4}LC + \left( {25{R^2}{C^2} - 50LC} \right){\omega ^2} + 25 = 0\,\,\left( 1 \right)\end{array}\)
Hai tần số cho cùng giá trị hiệu dụng \({U_L} \to \) phương trình (1) có 2 nghiệm \({\omega _2}^2,{\omega _3}^2\)
Áp dụng định lí Vi – et cho phương trình (1), ta có:
\({\omega _2}^2{\omega _3}^2 = \dfrac{{25}}{{18{L^2}{C^2}}} = \dfrac{{25}}{{18}}{\omega _1}^4 = \dfrac{{25}}{{18}}.{\left( {\sqrt {45} } \right)^4} = 2812,5\)
Theo đề bài ta có hệ phương trình:
\(\left\{ \begin{array}{l}{\omega _2}^2 + 4{\omega _3}^2 = 225\\{\omega _2}^2{\omega _3}^2 = 2812,5\end{array} \right. \Rightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}{\omega _2}^2 = 75\,\,\left( {ra{d^2}/{s^2}} \right)\\{\omega _3}^2 = 37,5\,\,\left( {ra{d^2}/{s^2}} \right)\end{array} \right.\\\left\{ \begin{array}{l}{\omega _2}^2 = 150\,\,\left( {ra{d^2}/{s^2}} \right)\\{\omega _3}^2 = 18,75\,\,\left( {ra{d^2}/{s^2}} \right)\end{array} \right.\end{array} \right.\)
Điện áp hai đầu cuộn cảm đạt cực đại, ta có:
\(\dfrac{2}{{{\omega _4}^2}} = \dfrac{1}{{{\omega _2}^2}} + \dfrac{1}{{{\omega _3}^2}} \Rightarrow \left[ \begin{array}{l}{\omega _4}^2 = 50\,\,\left( {ra{d^2}/{s^2}} \right)\\{\omega _4}^2 = \dfrac{{100}}{3}\,\,\left( {ra{d^2}/{s^2}} \right)\end{array} \right.\)
Chọn A.
Câu hỏi 33 :
Đặt điện áp \(u = 220\sqrt 2 \cos 2\pi ft\,\,\left( V \right)\) (f thay đổi được) vào hai đầu đoạn mạch mắc nối tiếp gồm cuộn cảm thuần có độ tự cảm L, điện trở R và tụ điện có điện dung C, với \(C{R^2} < 2L\). Khi \(f = {f_1}\) thì điện áp hiệu dụng giữa hai đầu tụ điện đạt cực đại. Khi \(f = {f_2} = \sqrt 3 {f_1}\) thì điện áp hiệu dụng hai đầu điện trở cực đại. Khi \(f = {f_3}\) thì điện áp giữa hai đầu cuộn cảm đạt cực đại \({U_{L\left( {\max } \right)}}\). Giá trị của \({U_{L\left( {\max } \right)}}\) gần giá trị nào nhất sau đây?
- A 185 V.
- B 145 V.
- C 157 V.
- D 233 V.
Đáp án: D
Phương pháp giải:
Tần số góc \({\omega _1}\) khi điện áp giữa hai đầu tụ điện đạt cực đại, \({\omega _2}\) khi điện áp hiệu dụng giữa hai đầu cuộn dây đạt cực đại, điện áp hiệu dụng giữa hai đầu điện trở đạt cực đại khi: \({\omega _0}^2 = {\omega _1}{\omega _2}\)
Điện áp hiệu dụng giữa hai đầu cuộn cảm thuần: \({U_{L\max }} = \dfrac{U}{{\sqrt {1 - {n^{ - 2}}} }}\) với \(n = \dfrac{{{\omega _L}}}{{{\omega _C}}}\)
Lời giải chi tiết:
Tần số góc \({\omega _1}\) khi điện áp giữa hai đầu tụ điện đạt cực đại, \({\omega _2}\) khi điện áp hiệu dụng giữa hai đầu cuộn dây đạt cực đại, điện áp hiệu dụng giữa hai đầu điện trở đạt cực đại khi:
\(\begin{array}{l}{\omega _0}^2 = {\omega _1}{\omega _2} \Rightarrow {f_0} = {f_1}.{f_2} \Rightarrow {\left( {\sqrt 3 {f_1}} \right)^2} = {f_1}.{f_2} \Rightarrow {f_2} = 3{f_1}\\ \Rightarrow n = \dfrac{{{f_2}}}{{{f_1}}} = 3\end{array}\)
Điện áp hiệu dụng giữa hai đầu cuộn cảm thuần:
\({U_{L\max }} = \dfrac{U}{{\sqrt {1 - {n^{ - 2}}} }} = \dfrac{{220}}{{\sqrt {1 - {3^{ - 2}}} }} \approx 233\,\,\left( V \right)\)
Chọn D.
Câu hỏi 34 :
Đặt điện áp \(u = {U_0}\cos 2\pi ft\,\,\left( V \right)\) (f thay đổi được) vào hai đầu đoạn mạch mắc nối tiếp gồm cuộn cảm thuần có độ tự cảm L, điện trở R và tụ điện có điện dung C, với \(C{R^2} < 2L\). Lần lượt thay đổi sao cho \(f = {f_C}\) rồi \(f = {f_L}\) thì điện áp hiệu dụng trên tụ điện đạt cực đại rồi điện áp hiệu dụng trên cuộn cảm đạt cực đại. Khi \(4{f_L} = 5{f_C}\) thì hệ số công suất khi \(f = {f_L}\) có giá trị là
- A \(\dfrac{{2\sqrt 5 }}{3}\)
- B \(\dfrac{{2\sqrt 2 }}{3}\)
- C \(\dfrac{2}{{\sqrt 5 }}\)
- D \(\dfrac{2}{3}\)
Đáp án: B
Phương pháp giải:
Hệ số công suất của mạch khi điện áp hiệu dụng trên cuộn cảm đạt cực đại: \(\cos \varphi = \sqrt {\dfrac{2}{{\dfrac{{{\omega _L}}}{{{\omega _C}}} + 1}}} \)
Lời giải chi tiết:
Hệ số công suất của mạch khi điện áp hiệu dụng trên cuộn cảm đạt cực đại:
\(\cos \varphi = \sqrt {\dfrac{2}{{\dfrac{{{\omega _L}}}{{{\omega _C}}} + 1}}} = \sqrt {\dfrac{2}{{\dfrac{{{f_L}}}{{{f_C}}} + 1}}} = \sqrt {\dfrac{2}{{\dfrac{5}{4} + 1}}} = \dfrac{{2\sqrt 2 }}{3}\)
Chọn B.
Câu hỏi 35 :
Cho mạch điện xoay chiều mắc nối tiếp gồm các phần tử điện trở thuần R, cuộn dây thuần cảm có độ tự cảm L và tụ điện có điện dung C. Mạch chỉ có tần số góc thay đổi được. Khi \(\omega = {\omega _1} = 100\pi \,\,rad/s\) thì điện áp hiệu dụng hai đầu tụ điện cực đại. Khi \(\omega = {\omega _2} = 2{\omega _1}\) thì điện áp hiệu dụng hai đầu cuộn dây đạt cực đại. Biết khi \(\omega = {\omega _1}\) thì \({Z_L} + 3{Z_C} = 400\,\,\Omega \). Giá trị của L bằng
- A \(\dfrac{4}{{5\pi }}\,\,H\)
- B \(\dfrac{4}{{3\pi }}\,\,H\)
- C \(\dfrac{3}{{4\pi }}\,\,H\)
- D \(\dfrac{5}{{4\pi }}\,\,H\)
Đáp án: A
Phương pháp giải:
Tần số góc \({\omega _1}\) khi điện áp giữa hai đầu tụ điện đạt cực đại, \({\omega _2}\) khi điện áp hiệu dụng giữa hai đầu cuộn dây đạt cực đại, mạch có cộng hưởng khi: \({\omega _0}^2 = {\omega _1}{\omega _2}\)
Lời giải chi tiết:
Tần số góc \({\omega _1}\) khi điện áp giữa hai đầu cuộn cảm đạt cực đại, \({\omega _2}\) khi điện áp hiệu dụng giữa hai đầu tụ điện đạt cực đại, mạch có cộng hưởng khi:
\(\begin{array}{l}{\omega _0} = \sqrt {{\omega _1}{\omega _2}} = \sqrt {2{\omega _1}^2} = \sqrt 2 {\omega _1} = 100\sqrt 2 \pi \,\,\left( {rad/s} \right)\\ \Rightarrow {\omega _2} = \sqrt 2 {\omega _0} \Rightarrow \left[ \begin{array}{l}{Z_L} = \sqrt 2 {Z_{{L_0}}}\\{Z_C} = \dfrac{{{Z_{{C_0}}}}}{{\sqrt 2 }} = \dfrac{{{Z_{{L_0}}}}}{{\sqrt 2 }}\end{array} \right.\end{array}\)
Theo đề bài ta có:
\(\begin{array}{l}{Z_L} + 3{Z_C} = 400\,\,\Omega \Rightarrow \sqrt 2 {Z_{{L_0}}} + 3\dfrac{{{Z_{{L_0}}}}}{{\sqrt 2 }} = 400\\ \Rightarrow {Z_{{L_0}}} = {\omega _0}L = 80\sqrt 2 \Rightarrow L = \dfrac{4}{{5\pi }}\,\,\left( H \right)\end{array}\)
Chọn A.
Câu hỏi 36 :
Đoạn mạch nối tiếp AB gồm tụ điện có điện dung \(C = \dfrac{1}{{6\pi }}\,\,mF\), cuộn cảm có độ tự cảm \(L = \dfrac{{0,3}}{\pi }\,\,H\), có điện trở \(r = 10\,\,\Omega \) và một biến trở R. Đặt vào điện áp xoay chiều có tần số thay đổi được. Khi \(f = 50\,\,Hz\), thay đổi R thì điện áp hiệu dụng trên tụ đạt cực đại là \({U_1}\). Khi \(R = 30\,\,\Omega \), thay đổi f thì điện áp hiệu dụng trên tụ cực đại là \({U_2}\). Tỉ số \(\dfrac{{{U_1}}}{{{U_2}}}\) bằng:
- A 1,58
- B 3,15
- C 0,79
- D 6,29
Đáp án: A
Phương pháp giải:
Thay đổi R để điện áp hiệu dụng trên tụ cực đại: \({U_1} = \dfrac{{U.{Z_C}}}{{\sqrt {{r^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\)
Thay đổi tần số để điện áp hiệu dụng trên tụ cực đại: \({U_2} = \dfrac{U}{{\sqrt {1 - {n^{ - 2}}} }}\) với \({n^{ - 1}} = 1 - \dfrac{{C{{\left( {R + r} \right)}^2}}}{{2L}}\)
Lời giải chi tiết:
Khi \(f = 50\,\,Hz\), dung kháng và cảm kháng của mạch điện là:
\(\left\{ \begin{array}{l}{Z_L} = 2\pi fL = 2\pi .50.\dfrac{{0,3}}{\pi } = 30\,\,\left( \Omega \right)\\{Z_C} = \dfrac{1}{{2\pi C}} = \dfrac{1}{{2\pi .50.\dfrac{{{{10}^{ - 3}}}}{6}}} = 60\,\,\left( \Omega \right)\end{array} \right.\)
Điện áp hiệu dụng cực đại giữa hai đầu tụ điện khi đó là:
\({U_1} = \dfrac{{U.{Z_C}}}{{\sqrt {{r^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = \dfrac{{U.60}}{{\sqrt {{{10}^2} + {{\left( {30 - 60} \right)}^2}} }} = \dfrac{{6U}}{{\sqrt {10} }}\)
Ta có: \({n^{ - 1}} = 1 - \dfrac{{C{{\left( {R + r} \right)}^2}}}{{2L}} = 1 - \dfrac{{\dfrac{{{{10}^{ - 3}}}}{{6\pi }}.{{\left( {30 + 10} \right)}^2}}}{{2.\dfrac{{0,3}}{\pi }}} = \dfrac{5}{9}\)
Điện áp hiệu dụng cực đại trên tụ là:
\({U_2} = \dfrac{U}{{\sqrt {1 - {n^{ - 2}}} }} = \dfrac{U}{{\sqrt {1 - {{\left( {\dfrac{5}{9}} \right)}^2}} }} = \dfrac{{9U}}{{2\sqrt {14} }} \Rightarrow \dfrac{{{U_1}}}{{{U_2}}} = \dfrac{{\dfrac{{6U}}{{\sqrt {10} }}}}{{\dfrac{{9U}}{{2\sqrt {14} }}}} \approx 1,58\)
Chọn A.
Câu hỏi 37 :
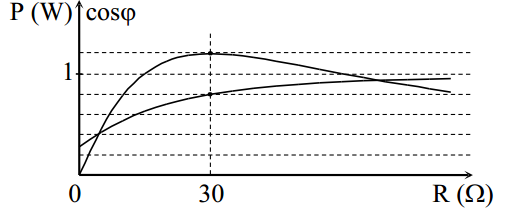
Đặt điện áp xoay chiều có giá trị hiệu dụng và tần số không đổi vào hai đầu đoạn mạch gồm biến trở, cuộn dây và tụ điện mắc nối tiếp. Hình vẽ bên là đồ thị biểu diễn sự phụ thuộc của công suất tỏa nhiệt P trên biến trở và hệ số công suất cosφ của đoạn mạch theo giá trị R của biến trở. Điện trở của cuộn dây có giá trị gần nhất với giá trị nào sau đây?
- A 9,1 Ω.
- B 10,1 Ω.
- C 7,9 Ω
- D 11,2 Ω.
Đáp án: C
Phương pháp giải:
Công thức tính công suất \(P = UI.\cos \varphi = {I^2}.R = \frac{{{U^2}}}{{{Z^2}}}.R\)
Bất đẳng thức Cô – si: \(a + b \ge 2\sqrt {ab} \)
Lời giải chi tiết:
Từ đồ thị ta thấy khi R = 30Ω thì hệ số công suất bằng 0,8 và công suất tiêu thụ của biến trở đạt cực đại
Ta có công thức tính công suất trên biến trở là:
\(P = {I^2}.R = \frac{{{U^2}}}{{{Z^2}}}.R = \frac{{{U^2}}}{{{{(R + r)}^2} + {{({Z_L} - {Z_C})}^2}}}.R = \frac{{{U^2}}}{{2r + R + \frac{{{r^2} + {{({Z_L} - {Z_C})}^2}}}{R}}} = \frac{{{U^2}}}{y} \Rightarrow {P_{\max }} \Leftrightarrow {y_{\min }}\)
Theo bất đẳng thức Cô – si ta có: \(R + \frac{{{r^2} + {{({Z_L} - {Z_C})}^2}}}{R} \ge 2.\sqrt {{r^2} + {{({Z_L} - {Z_C})}^2}} \)
Dấu “=” xảy ra khi: \({R^2} = {r^2} + {({Z_L} - {Z_C})^2}(*)\)
Lại có: \(\cos \varphi = \frac{{R + r}}{Z} = 0,8 \Rightarrow R + r = 0,8Z \Rightarrow |({Z_L} - {Z_C})| = 0,6Z \Rightarrow 0,6(R + r) = 0,8.|{Z_L} - {Z_C}|(**)\)
Từ (*) và (**) \( \Rightarrow {R^2} - {r^2} = \frac{{0,36}}{{0,64}}{(R + r)^2} \Leftrightarrow 0,64(R - r) = 0,36(R + r) \Rightarrow r = 0,28R = 0,28.30 = 8,4\Omega \)
Vậy giá trị gần nhất với 8,4 trong 4 đáp án là C. 7,9
Câu hỏi 38 :
Đoạn mạch xoay chiều AB có RLC nối tiếp, cuộn dây thuần cảm với \(C{R^2} < 2L\), điện áp hai đầu đoạn mạch là \({u_{AB}} = U\sqrt 2 \cos \omega t\,\,\left( V \right)\), \(U\) ổn định và \(\omega \) thay đổi. Khi \(\omega = {\omega _C}\) thì điện áp hai đầu tụ C cực đại, khi đó điện áp tức thời giữa hai đầu đoạn mạch AN (gồm RL) và AB lệch pha nhau là \(\alpha \). Giá trị nhỏ nhất của \(\tan \alpha \) là
- A \(2\sqrt 2 \)
- B \(\dfrac{{\sqrt 2 }}{2}\)
- C \(2,5\)
- D \(\sqrt 3 \)
Đáp án: A
Phương pháp giải:
Tần số thay đổi để điện áp hiệu dụng trên tụ cực đại: \(\tan \varphi .\tan {\varphi _{RL}} = - \dfrac{1}{2}\)
Bất đẳng thức Cô – si: \(a + b \ge 2\sqrt {ab} \) (dấu “=” xảy ra \( \Leftrightarrow a = b\))
Lời giải chi tiết:
Tần số thay đổi để điện áp hiệu dụng trên tụ cực đại, ta có:
\(\tan \varphi .\tan {\varphi _{RL}} = - \dfrac{1}{2} \Rightarrow \tan \varphi = - \dfrac{1}{{2\tan {\varphi _{RL}}}}\)
Theo đề bài ta có độ lệch pha:
\(\begin{array}{l}\alpha = {\varphi _{RC}} - \varphi \Rightarrow \tan \alpha = \tan \left( {{\varphi _{RC}} - \varphi } \right) = \dfrac{{\tan {\varphi _{RC}} - \tan \varphi }}{{1 + \tan {\varphi _{RC}}.\tan \varphi }}\\ \Rightarrow \tan \alpha = \dfrac{{\tan {\varphi _{RC}} + \dfrac{1}{{2\tan {\varphi _{RC}}}}}}{{1 - \dfrac{1}{2}}} = 2\tan {\varphi _{RC}} + \dfrac{1}{{\tan {\varphi _{RC}}}}\end{array}\)
Áp dụng bất đẳng thức Cô – si, ta có:
\(\begin{array}{l}2\tan {\varphi _{RC}} + \dfrac{1}{{\tan {\varphi _{RC}}}} \ge 2\sqrt {2\tan {\varphi _{RC}}.\dfrac{1}{{\tan {\varphi _{RC}}}}} = 2\sqrt 2 \\ \Rightarrow \tan \alpha \ge 2\sqrt 2 \Rightarrow {\left( {\tan \alpha } \right)_{\min }} = 2\sqrt 2 \end{array}\)
Chọn A.
Câu hỏi 39 :
Đặt điện áp xoay chiều tần số 50 Hz vào hai đầu đoạn mạch AB gồm hai đoạn mạch AM và MB mắc nối tiếp. Đoạn AM gồm điện trở thuần R = \(100\sqrt3 \Omega\)mắc nối tiếp với cuộn cảm thuần có độ tự cảm L, đoạn MB chỉ có tụ điện có điện dung C = 0,05/π (mF). Biết điện áp giữa hai đầu đoạn mạch MB và điện áp giữa hai đầu đoạn mạch AB lệch pha nhau π/3. Giá trị L bằng
- A 2/π (H).
- B 1/π (H).
- C \(\sqrt3\)/π (H).
- D 3/π (H).
Đáp án: B
Lời giải chi tiết:
\(\left\{ \matrix{
{Z_C} = {1 \over {\omega C}} = 200\left( \Omega \right) \hfill \cr
\Delta AEB:BE = AE.{\mathop{\rm c}\nolimits} otan{\pi \over 3} = 100\left( \Omega \right) \Rightarrow {Z_L} = {Z_C} - BE = 100\left( \Omega \right) \Rightarrow L = {{{Z_L}} \over \omega } = {1 \over \pi }\left( H \right) \hfill \cr} \right.\)
Câu hỏi 40 :
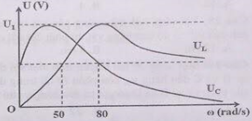
Đặt điện áp xoay chiều \(u = 60\sqrt 2 \cos \left( {\omega t} \right)\left( V \right)\), (ω thay đổi được) vào hai đầu đoạn mạch gồm điện trở R, cuộn dây thuần cảm và tụ điện mắc nối tiếp. Hình bên là đồ thị biểu diễn sự phụ thuộc của điện áp hiệu dụng hai đầu tụ điện UC và điện áp hiệu dụng hai đầu cuộn dây UL theo tần số góc. Giá trị của U1 là :
- A 60V
- B 80V
- C 90V
- D 100V
Đáp án: D
Phương pháp giải:
Sử dụng lí thuyết về mạch điện xoay chiều có ω thay đổi
+ Có 2 giá trị của ω để UC bằng nhau là ω1 và ω2 → Giá trị ωC để UCmax là :
\(\omega _C^2 = {1 \over 2}\left( {\omega _1^2 + \omega _2^2} \right)\)
+ Có 2 giá trị của ω để UL bằng nhau là ω1 và ω2 → Giá trị ωL để ULmax là :
\({2 \over {\omega _L^2}} = {1 \over {\omega _1^2}} + {1 \over {\omega _2^2}}\)
Lời giải chi tiết:
- Từ đồ thị ta thấy :
+ Có 2 giá trị của ω để UC bằng nhau là
\(\left[ \matrix{
{\omega _1} = 0 \hfill \cr
{\omega _2} = 80rad/s \hfill \cr} \right.\)
→ Giá trị ωC để UCmax là : \(\omega _C^2 = {1 \over 2}\left( {\omega _1^2 + \omega _2^2} \right) = {1 \over 2}\left( {{0^2} + {{80}^2}} \right) \Rightarrow {\omega _C} = 40\sqrt 2 \left( {rad/s} \right)\)
+ Có 2 giá trị của ω để UL bằng nhau là
\(\left[ \matrix{
{\omega _1} = 50rad/s \hfill \cr
{\omega _2} = \infty \hfill \cr} \right.\)
→ Giá trị ωL để ULmax là : \({2 \over {\omega _L^2}} = {1 \over {\omega _1^2}} + {1 \over {\omega _2^2}} = {1 \over {{{50}^2}}} + {1 \over {{\infty ^2}}} \Rightarrow {\omega _L} = 50\sqrt 2 \left( {rad/s} \right)\)
- Mặt khác áp dụng công thức :
\({U_{L\max }} = {U_{C\max }} = {U \over {\sqrt {1 - {{\left( {{{{\omega _L}} \over {{\omega _C}}}} \right)}^2}} }} = {{60} \over {\sqrt {1 - {{\left( {{{50\sqrt 2 } \over {40\sqrt 2 }}} \right)}^{ - 2}}} }} = 100V\)
Chọn D
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Các bài khác cùng chuyên mục
- 50 bài tập Ôn tập chương 3: Dòng điện xoay chiều mức độ vận dụng cao
- 50 bài tập Ôn tập chương 3: Dòng điện xoay chiều mức độ vận dụng (Phần 1)
- 50 bài tập Động cơ không đồng bộ ba pha mức độ vận dụng
- 50 bài tập Máy phát điện xoay chiều mức độ vận dụng
- 50 bài tập Máy phát điện xoay chiều mức độ nhận biết, thông hiểu
- 50 bài tập Ôn tập chương 3: Dòng điện xoay chiều mức độ vận dụng cao
- 50 bài tập Ôn tập chương 3: Dòng điện xoay chiều mức độ vận dụng (Phần 1)
- 50 bài tập Động cơ không đồng bộ ba pha mức độ vận dụng
- 50 bài tập Máy phát điện xoay chiều mức độ vận dụng
- 50 bài tập Máy phát điện xoay chiều mức độ nhận biết, thông hiểu