 Giải toán 10, giải bài tập toán lớp 10 đầy đủ đại số và hình học
Giải toán 10, giải bài tập toán lớp 10 đầy đủ đại số và hình học
 Đề kiểm tra 15 phút - Chương 1 - Hình học 10
Đề kiểm tra 15 phút - Chương 1 - Hình học 10
Đề kiểm tra 15 phút - Chương 1 - Đề số 4 - Hình học 10
Đáp án và lời giải chi tiết Đề kiểm tra 15 phút - Chương 1 - Đề số 4 - Hình học 10
Đề bài
Chọn phương án đúng
Câu 1. Cho tam giác đều ABC có cạnh bằng a. Độ dài của véctơ \(\overrightarrow {BA} + \overrightarrow {BC} \) là
A.2a
B.\({{a\sqrt 3 } \over 2}\)
C.a
D.\(a\sqrt 3 \)
Câu 2. Cho tam giác ABC vuông tại A có AB=6, AC=8. Độ dài của véctơ \(\overrightarrow {BA} + \overrightarrow {BC} \) là
A.\(2\sqrt 3 \)
B.10
C.\(4\sqrt {13} \)
D.16
Câu 3. Cho tam giác đều ABC có cạnh bằng 3. Gọi I là trung điểm của BC. Độ dài véctơ \(\overrightarrow {CA} - \overrightarrow {IC} \) là
A.\(\dfrac{3 }{ 2}\)
B. \(\dfrac{3\sqrt 7 } {2}\)
C.\(2\sqrt 3 \)
D.\(\dfrac{9 }{ 2}\)
Câu 4. Cho tam giác ABC vuông tại A có BC = 15. Gọi G là trọng tâm. Độ dài của véctơ \(\overrightarrow {GB} + \overrightarrow {GC} \) là
A.10 B.5
C.15 D.20
Câu 5. Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của AB, CD. Tìm mệnh đề sai
A.\(\overrightarrow {AB} + \overrightarrow {CD} = 2\overrightarrow {MN} \)
B. \(\overrightarrow {AC} + \overrightarrow {DB} = 2\overrightarrow {MN} \)
C.\(\overrightarrow {AD} + \overrightarrow {BC} = 2\overrightarrow {MN} \)
D. \(\overrightarrow {CA} - \overrightarrow {BD} = 2\overrightarrow {NM} \)
Câu 6. Cho lục giác ABCDEF. Tìm mệnh đề đúng
A.\(\overrightarrow {AD} + \overrightarrow {BE} + \overrightarrow {CF} = \overrightarrow {AF} + \overrightarrow {BD} + \overrightarrow {CD} \)
B.\(\overrightarrow {AD} + \overrightarrow {BE} + \overrightarrow {CF} = \overrightarrow {AE} + \overrightarrow {BF} + \overrightarrow {CE} \)
C.\(\overrightarrow {AD} + \overrightarrow {BE} + \overrightarrow {CF} = \overrightarrow {AD} + \overrightarrow {BF} + \overrightarrow {CF} \)
D.\(\overrightarrow {AD} + \overrightarrow {BE} + \overrightarrow {CF} = \overrightarrow {AF} + \overrightarrow {BD} + \overrightarrow {CE} \)
Câu 7. Cho tam giác OAB. Gọi M, N lần lượt là trung điểm OA, OB . Tìm mệnh đề đúng
A.\(\overrightarrow {MN} = \dfrac{1 }{ 2}\overrightarrow {OA} + \dfrac{1 }{ 2}\overrightarrow {OB} \)
B. \(\overrightarrow {MN} = \dfrac{1}{2}\overrightarrow {OB} - \dfrac{1 }{ 2}\overrightarrow {OA} \)
C. \(\overrightarrow {MN} = \dfrac{1}{2}\overrightarrow {OA} - \dfrac{1 }{2}\overrightarrow {OB} \)
D.\(\overrightarrow {MN} = \overrightarrow {OA} + \overrightarrow {OB} \)
Câu 8. Cho hình bình hành ABCD. Gọi G là trọng tâm tam giác ABC. Tìm mệnh đề sai
A.\(\overrightarrow {DA} + \overrightarrow {DB} + \overrightarrow {DC} = 3\overrightarrow {DG} \)
B.\(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GD} = \overrightarrow {CD} \)
C.\(\overrightarrow {DA} + \overrightarrow {DB} + \overrightarrow {DC} = \overrightarrow {DG} \)
D.\(\overrightarrow {GA} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow {BD} \)
Câu 9. Cho hình bình hành ABCD và \(AB'C'D'\) có chung đỉnh A. Tìm mệnh đề đúng
A.\(BCC'B'\) là hình bình hành
B.\(\overrightarrow {CC'} = \overrightarrow {BB'} + \overrightarrow {DD'} \)
C.\(C{\rm{DD}}'C'\) là hình bình hành
D.\(\overrightarrow {AC} = \overrightarrow {AC'} \)
Câu 10. Tam giác ABC là tam giác gì nếu thỏa mãn điều kiện \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AB} - \overrightarrow {AC} } \right|\) ?
A.Vuông B. Cân
C. Đều D. Nhọn
Lời giải chi tiết
Câu 1.D
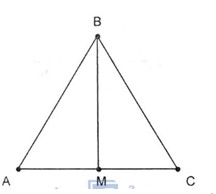
Gọi M là trung điểm AC. Khi đó \(\overrightarrow {BA} + \overrightarrow {BC} = 2\overrightarrow {BM} \) .
Mà \(BM = \dfrac{a\sqrt 3 } { 2}\) . Do đó \(\left| {\overrightarrow {BA} + \overrightarrow {BC} } \right| = \left| {2\overrightarrow {BM} } \right| = 2BM = a\sqrt 3 \) .
Câu 2.C
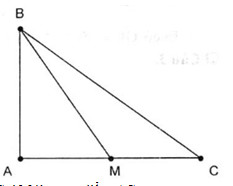
Gọi M là trung điểm AC.
Khi đó \(\overrightarrow {BA} + \overrightarrow {BC} \)\(\,= 2\overrightarrow {BM} \) .
Mà \(BM = \sqrt {A{B^2} + A{M^2}} = \sqrt {36 + 16} \)\(\,= 2\sqrt {13} \) .
Do đó \(\left| {\overrightarrow {BA} + \overrightarrow {BC} } \right| = \left| {2\overrightarrow {BM} } \right| = 2BM \)\(\,= 4\sqrt {13} \) .
Câu 3.B
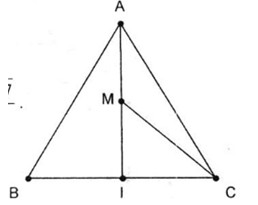
Gọi M là trung điểm AI.
Theo Pitago ta có:
\(AI = \sqrt {A{C^2} - I{C^2}} \)\( = \sqrt {{3^2} - {{\left( {\frac{3}{2}} \right)}^2}} = \frac{{3\sqrt 3 }}{2} \)
\(\Rightarrow MI = \frac{1}{2}AI = \frac{{3\sqrt 3 }}{4}\)
Khi đó \(\overrightarrow {CA} - \overrightarrow {IC} = \overrightarrow {CA} + \overrightarrow {CI} = 2\overrightarrow {CM} \) .
Mà \(CM = \sqrt {C{I^2} + M{I^2}} \)\(\; = \sqrt {{{\left( {\dfrac{3}{2}} \right)}^2} + {{\left( {\dfrac{{3\sqrt 3 }}{4}} \right)}^2}} = \dfrac{{3\sqrt 7 }}{4}\).
Vậy \(\left| {\overrightarrow {CA} - \overrightarrow {IC} } \right| = \left| {2\overrightarrow {CM} } \right| = 2CM = \dfrac{3\sqrt 7 }{ 2}\) .
Câu 4.B
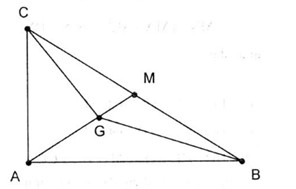
Gọi M là trung điểm BC.
Ta có \(\overrightarrow {GB} + \overrightarrow {GC} = 2\overrightarrow {GM} \) .
Mà \(GM = \dfrac{1}{3}AM = \dfrac{1}{6}BC = \dfrac{{15}}{6} = \dfrac{5}{2}\).
Do đó \(\left| {\overrightarrow {GB} + \overrightarrow {GC} } \right| = \left| {2\overrightarrow {GM} } \right| = 2GM = 5\) .
Câu 5.A
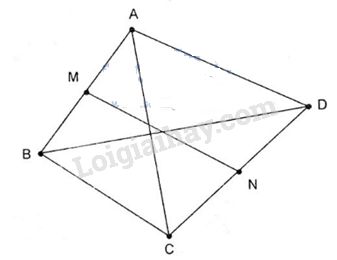
Ta có
\(\overrightarrow {AC} + \overrightarrow {BD} \)
\(= \overrightarrow {AM} + \overrightarrow {MN} + \overrightarrow {NC} + \overrightarrow {BM} + \overrightarrow {MN} + \overrightarrow {ND} \)
\(= 2\overrightarrow {MN} + \left( {\overrightarrow {AM} + \overrightarrow {BM} } \right) + \left( {\overrightarrow {NC} + \overrightarrow {ND} } \right) \)
\(= 2\overrightarrow {MN} \)
Suy ra (B) là mệnh đề đúng.
Tương tự
\(\overrightarrow {AD} + \overrightarrow {BC} \)
\(= \overrightarrow {AM} + \overrightarrow {MN} + \overrightarrow {ND} + \overrightarrow {BM} + \overrightarrow {MN} + \overrightarrow {NC} \)
\( = 2\overrightarrow {MN} + \left( {\overrightarrow {AM} + \overrightarrow {BM} } \right) + \left( {\overrightarrow {NC} + \overrightarrow {ND} } \right)\)
\(= 2\overrightarrow {MN} \)
Vậy (C) là mệnh đề đúng.
Cũng vậy:
\(\overrightarrow {CA} - \overrightarrow {BD} \)\(\,= \overrightarrow {CN} + \overrightarrow {MN} + \overrightarrow {MA} - \left( {\overrightarrow {BM} + \overrightarrow {MN} + \overrightarrow {ND} } \right)\)
\( = 2\overrightarrow {MN} + \left( {\overrightarrow {MA} + \overrightarrow {MB} } \right) + \left( {\overrightarrow {CN} + \overrightarrow {DN} } \right)\)\( = 2\overrightarrow {MN} \)
Do đó (D) là mệnh đề đúng.
Câu 6.D
\(\overrightarrow {AD} + \overrightarrow {BE} + \overrightarrow {CF} \)
\(= \overrightarrow {AF} + \overrightarrow {FD} + \overrightarrow {BD} + \overrightarrow {DE} + \overrightarrow {CE} + \overrightarrow {EF} \)
\( = \overrightarrow {AF} + \overrightarrow {BD} + \overrightarrow {CE} + \overrightarrow {FD} + \overrightarrow {DE} + \overrightarrow {EF} \)
Chú ý kết quả đúng khi thứ tự các điểm đầu được giữ nguyên, chỉ hoán vị vòng quanh các điểm cuối.
Câu 7.B
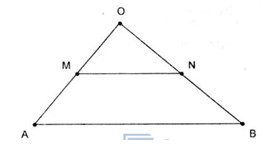
Ta có \(\overrightarrow {MN} = \overrightarrow {ON} - \overrightarrow {OM} = {1 \over 2}\overrightarrow {OB} - {1 \over 2}\overrightarrow {OA} \) .
Vậy (B) đúng.
Câu 8.C
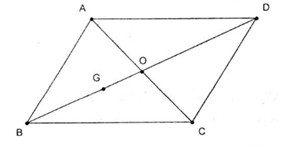
Hiển nhiên \(\overrightarrow {DA} + \overrightarrow {DB} + \overrightarrow {DC} = 3\overrightarrow {DG} \) .
Mặt khác
\(\eqalign{ & \overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GD} \cr&= \overrightarrow {GA} + \overrightarrow {GB} - 2\overrightarrow {GB} \cr & {\rm{ }} = \overrightarrow {GA} - \overrightarrow {GB} = \overrightarrow {BA} = \overrightarrow {CD} \cr} \) .
Tương tự \(\overrightarrow {GA} + \overrightarrow {GC} + \overrightarrow {GD} = 2\overrightarrow {GO} + \overrightarrow {GD} \)\(\,= \overrightarrow {GD} - \overrightarrow {GB} = \overrightarrow {BD} \) .
Vậy (A), (B), (D) là các mệnh đề đúng
Câu 9.B
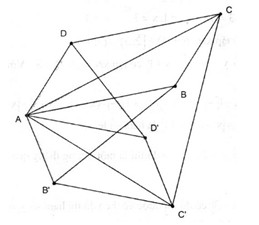
Ta có:
\(\overrightarrow {BB'} + \overrightarrow {DD'} \)
\(\;= \overrightarrow {AB'} - \overrightarrow {AB} + \overrightarrow {AD'} - \overrightarrow {AD} \)
\(\eqalign{ & = \left( {\overrightarrow {AB'} + \overrightarrow {AD'} } \right) - \left( {\overrightarrow {AB} + \overrightarrow {AD} } \right) \cr & = \overrightarrow {AC'} - \overrightarrow {AC} = \overrightarrow {CC'} \cr} \) .
Câu 10.A
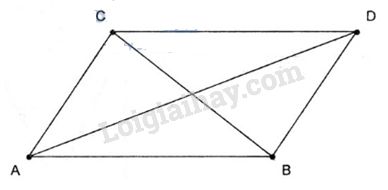
Vẽ hình bình hành ABDC.
Ta có \(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AD} ,{\rm{ }}\overrightarrow {AB} - \overrightarrow {AC} = \overrightarrow {CB} \) .
Do đó \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AB} - \overrightarrow {AC} } \right| \)\(\,\Leftrightarrow AD = CB \Leftrightarrow ABDC\) là hình chữ nhật.
Vậy ABC là tam giác vuông tại A.
Loigiaihay.com












Danh sách bình luận