 Giải toán 10, giải bài tập toán lớp 10 đầy đủ đại số và hình học
Giải toán 10, giải bài tập toán lớp 10 đầy đủ đại số và hình học
 Đề kiểm tra 15 phút - Chương 1 - Hình học 10
Đề kiểm tra 15 phút - Chương 1 - Hình học 10
Đề kiểm tra 15 phút - Chương 1 - Đề số 1 - Hình học 10
Đáp án và lời giải chi tiết Đề kiểm tra 15 phút - Chương 1 - Đề số 1 - Hình học 10
Đề bài
Câu 1. Cho tam giác ABC vuông tại A có trọng tâm là G. Biết rằng AB=6 và AC=8. Tính độ dài của các véc tơ \(\overrightarrow {GB} - \overrightarrow {GC} \) và \(\overrightarrow {GB} + \overrightarrow {GC} \).
Câu 2. Cho hai hình bình hành ABCD và AMNP có chung đỉnh A. Chứng minh rằng \(\overrightarrow {BM} + \overrightarrow {DP} = \overrightarrow {CN} \).
Câu 3. Cho hình bình hành ABDC tâm O. Gọi G là trọng tâm tam giác OCD. Hãy biểu thị \(\overrightarrow {BG} \) theo các véc tơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \).
Lời giải chi tiết
Câu 1.
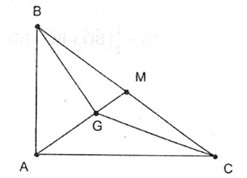
Theo định lí Pitago ta có: \(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {36 + 64} = 10\)
Ta có \(\overrightarrow {GB} - \overrightarrow {GC} = \overrightarrow {CB} \) . Suy ra \(\left| {\overrightarrow {GB} - \overrightarrow {GC} } \right| = \left| {\overrightarrow {CB} } \right| = CB = 10\)
Gọi M là trung điểm BC. Ta có \(\overrightarrow {GB} + \overrightarrow {GC} = 2\overrightarrow {GM} \) .
Mà \(GM = \dfrac{1 }{3}AM = \dfrac{1 }{6}BC = \dfrac{10} {6} = \dfrac{5 }{ 3}\)
Vậy \(\left| {\overrightarrow {GB} + \overrightarrow {GC} } \right| = \left| {2\overrightarrow {GM} } \right| = 2GM = \dfrac{10}{3}\)
Câu 2.
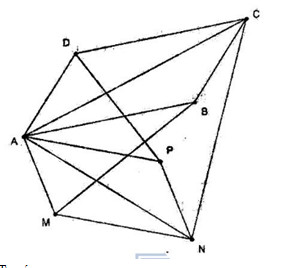
Ta có
\(\overrightarrow {BM} + \overrightarrow {DP} \)
\(= \overrightarrow {AM} - \overrightarrow {AB} + \overrightarrow {AP} - \overrightarrow {AD} \)
\( = \left( {\overrightarrow {AM} + \overrightarrow {AP} } \right) - \left( {\overrightarrow {AB} + \overrightarrow {AD} } \right) \)
\(= \overrightarrow {AN} - \overrightarrow {AC} = \overrightarrow {CN} \)
Câu 3.
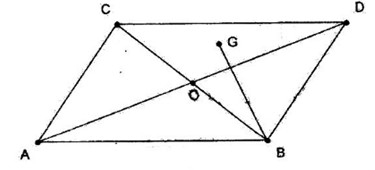
Ta có:
\(\eqalign{ & \overrightarrow {BG} = \dfrac{1}{3}\left( {\overrightarrow {BO} + \overrightarrow {BC} + \overrightarrow {BD} } \right) \cr } \)
\(\begin{array}{l}
= \dfrac{1}{3}\left( {\dfrac{1}{2}\overrightarrow {BC} + \overrightarrow {BC} + \overrightarrow {AC} } \right)\\
= \dfrac{1}{3}\left( {\dfrac{3}{2}\overrightarrow {BC} + \overrightarrow {AC} } \right)\\
= \dfrac{1}{2}\overrightarrow {BC} + \dfrac{1}{3}\overrightarrow {AC} \\
= \dfrac{1}{2}\left( {\overrightarrow {AC} - \overrightarrow {AB} } \right) + \dfrac{1}{3}\overrightarrow {AC} \\
= \dfrac{1}{2}\overrightarrow {AC} - \dfrac{1}{2}\overrightarrow {AB} + \dfrac{1}{3}\overrightarrow {AC} \\
= - \dfrac{1}{2}\overrightarrow {AB} + \dfrac{5}{6}\overrightarrow {AC}
\end{array}\)
Loigiaihay.com












Danh sách bình luận