Đề kiểm tra 15 phút - Chương 1 - Đề số 2 - Hình học 10

Đề bài

Chọn phương án đúng

Câu 1. Cho tam giác ABC với M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC. Véc tơ đối của véc tơ \(\overrightarrow {MN} \) là

A.\(\overrightarrow {BP} \)        B.\(\overrightarrow {MA} \)                          

C.\(\overrightarrow {PC} \)        D.\(\overrightarrow {PB} \)

Câu 2. Cho ba điểm A, B, C phân biệt. Đẳng thức nào sau đây là sai ?

A.\(\overrightarrow {AB}  - \overrightarrow {BC}  = \overrightarrow {AC} \)          

B.\(\overrightarrow {AB}  + \overrightarrow {BC}  = \overrightarrow {AC} \)

C.\(\overrightarrow {BC}  + \overrightarrow {AB}  = \overrightarrow {AC} \)

D.\(\overrightarrow {BC}  - \overrightarrow {BA}  = \overrightarrow {AC} \)

Câu 3. Cho hình bình hành ABCD có tâm O. Khi đó ta có

A.\(\overrightarrow {AO}  - \overrightarrow {BO}  = \overrightarrow {BA} \) 

B.\(\overrightarrow {OA}  - \overrightarrow {OB}  = \overrightarrow {BA} \)

C.\(\overrightarrow {OA}  - \overrightarrow {OB}  = \overrightarrow {AB} \)

D.\(\overrightarrow {AO}  + \overrightarrow {BO}  = \overrightarrow {AB} \)

Câu 4. Cho hình vuông ABCD. Khi đó ta có

A.\(\overrightarrow {AB}  =  - \overrightarrow {BC} \)            

B.\(\overrightarrow {AD}  =  - \overrightarrow {BC} \)                

C.\(\overrightarrow {AC}  =  - \overrightarrow {BD} \)            

D.\(\overrightarrow {AD}  =  - \overrightarrow {CB} \)

Câu 5. Cho hai điểm phân biệt M, N. Điều kiện cần và đủ để P là trung điểm của đoạn MN là

A\(\overrightarrow {PM}  =  - \overrightarrow {PN} \)

B.\( PM=PN\)

C.\(\overrightarrow {PM}  = \overrightarrow {PN} \)

D.\(\overrightarrow {MP}  = \overrightarrow {NP} \)

Câu 6. Cho G là trọng tâm của tam giác ABC và M là trung điểm của đoạn BC. Đẳng thức nào sau đây sai ?

A.\(\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  = \overrightarrow 0 \)

B.\(\overrightarrow {AB}  + \overrightarrow {AC}  = 2\overrightarrow {AM} \)

C.\(\overrightarrow {GB}  + \overrightarrow {GC}  = 2\overrightarrow {GM} \)

D.\(\overrightarrow {BM}  + \overrightarrow {MC}  = \overrightarrow 0 \)

Câu 7. Gọi I là giao điểm của hai đường chéo của hình bình hành ABCD. Khi đó

A.\(\overrightarrow {AI}  = \dfrac{1 }{ 2}\overrightarrow {AB}  + \dfrac{1 }{ 2}\overrightarrow {AC} \)

B.\(\overrightarrow {AI}  = \dfrac{1 }{3}\overrightarrow {AB}  + \dfrac{1 }{3}\overrightarrow {AD} \)

C.\(\overrightarrow {AI}  = \dfrac{1 }{2}\overrightarrow {AB}  + \dfrac{1 }{ 2}\overrightarrow {AD} \)

D.\(\overrightarrow {AI}  = \dfrac{1 }{ 2}\overrightarrow {AB}  + \overrightarrow {BI} \)

Câu 8. Cho tam giác ABC. Gọi M là điểm trên đoạn BC sao cho MB = 2MC.

Khi đó

A.\(\overrightarrow {AM}  = \dfrac{1 }{ 3}\overrightarrow {AB}  + \overrightarrow {AC} \)

B.\(\overrightarrow {AM}  = \dfrac{1 }{3}\overrightarrow {AB}  + \dfrac{2 }{ 3}\overrightarrow {AC} \)

C.\(\overrightarrow {AM}  = \dfrac{1 }{3}\overrightarrow {AB}  + \dfrac{1 }{ 3}\overrightarrow {AC} \)

D.\(\overrightarrow {AM}  = \dfrac{1 }{3}\overrightarrow {AB}  + 2\overrightarrow {AC} \)

Câu 9. Cho tam giác đều ABC có cạnh bằng a, M là trung điểm của BC. Véc tơ \(\overrightarrow {CA}  - \overrightarrow {MC} \) có độ lớn là

A.\(\dfrac{{3a}}{2}\)

B. \(\dfrac{a}{2}\)

C. \(\dfrac{{2a\sqrt 3 }}{3}\)

D. \(\dfrac{{a\sqrt 7 }}{2}\)

Câu 10. Cho tam giác ABC vuông tại B có AB = 3cm, BC = 4cm. Độ dài của véctơ tổng \(\overrightarrow {AB}  + \overrightarrow {AC} \) là

A.\(\sqrt {13} \)cm   

B. \(13\) cm                      

C. \(2\sqrt {13} \) cm 

D. \(26\) cm

Lời giải chi tiết

Câu 1.D

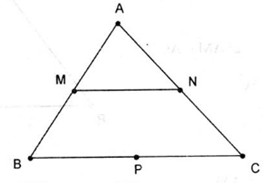
Véctơ đối của véctơ \(\overrightarrow {MN} \) là véctơ \(\overrightarrow {PB} \) .

Câu 2.A.

Ta có \(\overrightarrow {AB}  - \overrightarrow {AC}  = \overrightarrow {CB} \)

\(\Rightarrow \overrightarrow {AC}  = \overrightarrow {AB}  - \overrightarrow {CB}  \ne \overrightarrow {AB}  - \overrightarrow {BC} \)

Câu 3.B

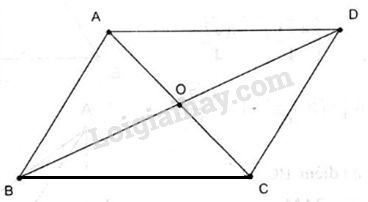
Theo quy tắc của phép trừ ta có \(\overrightarrow {OB}  - \overrightarrow {OA}  = \overrightarrow {AB} \) .

Câu 4. D

ABCD là hình vuông nên \(\overrightarrow {AD}  = \overrightarrow {BC} =  - \overrightarrow {CB} \)

Câu 5.A.

Ta có P là trung điểm \(MN \Leftrightarrow \overrightarrow {PM}  + \overrightarrow {PN}  = 0 \)

\(\Leftrightarrow \overrightarrow {PM}  =  - \overrightarrow {PN} \) .

Câu 6.D

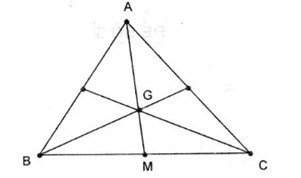
Ta có \(\overrightarrow {BM}  + \overrightarrow {MC}  = \overrightarrow {BC}  \ne \overrightarrow 0 \) .

Câu 7.C

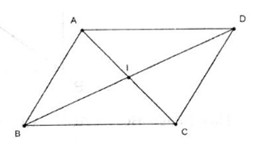
Ta có: \(\overrightarrow {AB}  + \overrightarrow {AD}  = 2\overrightarrow {AI}  \)

Suy ra \(\overrightarrow {AI}  = \dfrac{1 }{ 2}\overrightarrow {AB}  + \dfrac{1 }{ 2}\overrightarrow {AD}\)

Câu 8.B

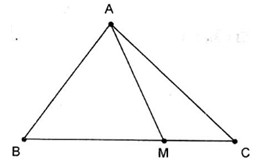
Ta có \(\overrightarrow {BM}  = \overrightarrow {AM}  - \overrightarrow {AB} ,\) \({\rm{ }}\overrightarrow {CM}  = \overrightarrow {AM}  - \overrightarrow {AC} \).

Mà \(\overrightarrow {BM}  =  - 2\overrightarrow {CM} \) .

Suy ra \(\overrightarrow {AM}  - \overrightarrow {AB}  =  - 2\left( {\overrightarrow {AM}  - \overrightarrow {AC} } \right)\) .

\( \Rightarrow 3\overrightarrow {AM}  = \overrightarrow {AB}  + 2\overrightarrow {AC} \)

\( \Rightarrow \overrightarrow {AM}  = \dfrac{1 }{ 3}\overrightarrow {AB}  +\dfrac{2 }{3}\overrightarrow {AC} \)

Câu 9. D

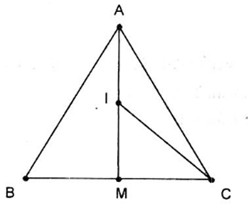
Gọi I là trung điểm AM.

Tam giác ACM vuông tại M nên theo Pitago ta có:

\(AM = \sqrt {A{C^2} - M{C^2}}  \)

\(= \sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 3 }}{2} \)

\(\Rightarrow MI = \frac{1}{2}AM = \frac{{a\sqrt 3 }}{4}\)

Ta có \(\overrightarrow {CA}  - \overrightarrow {MC}  = \overrightarrow {CA}  + \overrightarrow {CM}  = 2\overrightarrow {CI} .\)

\(\eqalign{
& CI = \sqrt {C{M^2} + M{I^2}} \cr
&= \sqrt {{{\left( {\frac{a}{2}} \right)}^2} + {{\left( {\frac{{a\sqrt 3 }}{4}} \right)}^2}} \cr
& = \frac{{a\sqrt 7 }}{4}. \cr} \)

Vậy \(\left| {\overrightarrow {CA}  - \overrightarrow {MC} } \right| = \left| 2{\overrightarrow {CI} } \right| = 2CI = {{a\sqrt 7 } \over 2}.\)

Câu 10. C

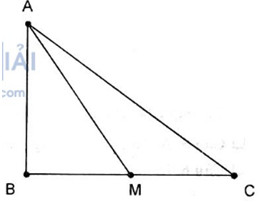
Gọi M là trung điểm BC. Ta có \(\overrightarrow {AB}  + \overrightarrow {AC}  = 2\overrightarrow {AM} \) .

Mà \(AM = \sqrt {A{B^2} + B{M^2}} \)\(\, = \sqrt {9 + 4}  = \sqrt {13} \) cm.

Vậy \(\left| {\overrightarrow {AB}  + \overrightarrow {AC} } \right| = \left| {2\overrightarrow {AM} } \right| \)\(\,= 2AM = 2\sqrt {13} \) cm.

 Loigiaihay.com