Câu hỏi
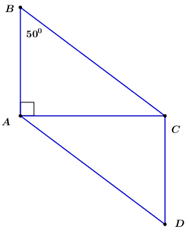
Cho tam giác ABC vuông tại A và có \(\angle B = {50^o}\). Hệ thức nào sau đây sai?
- A \(\left( {\overrightarrow {AB} ,\overrightarrow {CB} } \right) = {130^o}\)
- B \(\left( {\overrightarrow {AC} ,\overrightarrow {CB} } \right) = {140^o}\)
- C \(\left( {\overrightarrow {BC} ,\overrightarrow {AC} } \right) = {40^o}\)
- D \(\left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right) = {50^o}\)
Phương pháp giải:
Sử dụng định lý tổng 3 góc trong tam giác, tứ giác, đưa các vectơ về cùng một gốc để tìm góc giữa chúng.
Lời giải chi tiết:
Lấy điểm D sao cho ABCD là hình bình hành
\( \Rightarrow \left\{ \begin{array}{l}\angle BAD = \angle BCD\\\angle ABC = \angle CDA\end{array} \right.\) (tính chất hình bình hành)
\( \Rightarrow \angle BAD = \dfrac{{{{360}^o} - 2.\angle B}}{2} = {130^o}\) (định lý tổng 4 góc trong tứ giác)
Ta có \(\overrightarrow {BC} = \overrightarrow {AD} \) (ABCD là hình bình hành)
\( \Rightarrow \left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right) = \left( {\overrightarrow {AB} ,\overrightarrow {AD} } \right) = \angle BAD = {130^o}\)
Chọn D.