Phương pháp giải:

Sử dụng tính chất tam giác vuông cân, định lý Pytago.

Công thức tích vô hướng: \(\overrightarrow a .\overrightarrow b  = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\;\overrightarrow b } \right).\)

Lời giải chi tiết:

Ta có tam giác ABC vuông có \(AB = AC = 3\)

\( \Rightarrow \)Tam giác ABC vuông cân tại A.

\( \Rightarrow \angle ACB = \angle ABC = {45^o}\) (định lý tổng 3 góc trong tam giác)

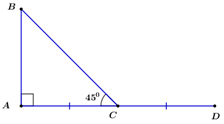
Gọi D là điểm đối xứng với A qua C \( \Rightarrow \angle BCD = {180^o} - \angle ACB = {135^o};\;CD = AC = 3;\;\overrightarrow {AC}  = \overrightarrow {CD} .\) 

Áp dụng định lý Pytago cho tam giác ABC vuông cân tại A\( \Rightarrow CB = \sqrt {A{B^2} + A{C^2}}  = 3\sqrt 2 \)

\(\overrightarrow {AC} .\overrightarrow {CB}  = \overrightarrow {CD} .\overrightarrow {CB}  = \left| {\overrightarrow {CD} } \right|.\left| {\overrightarrow {CB} } \right|.\cos \left( {\overrightarrow {CD} ,\overrightarrow {CB} } \right) = CD.CB.\cos \angle BCD = 3.3\sqrt 2 .\cos {135^o} =  - 9\)

Chọn B.