Câu hỏi
Trong mặt phẳng tọa độ\(Oxy\), cho hai điểm \(A\left( {1;2} \right)\) và \(B\left( {3;4} \right)\). Điểm \(M\left( {\dfrac{a}{b};0} \right)\) (với \(\dfrac{a}{b}\) là phân số tối giản) trên trục hoành thỏa mãn tổng khoảng cách từ P tới hai điểm A và B là nhỏ nhất. Tính \(S = a + b\).
- A \(S = - 2\)
- B \(S = 8\).
- C \(S = 7\).
- D \(S = 4\).
Phương pháp giải:
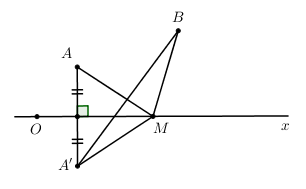
+) Nhận xét A, B nằm cùng phía so với trục Ox.
+) Lấy A’ đối xứng với A qua Ox ta có: \(MA + MB = MA' + MB \ge A'B\). Dấu "=" xảy ra \( \Leftrightarrow M = Ox \cap A'B\).
Lời giải chi tiết:
A(1,2) và B(3,4) nằm cùng phía đối với trục Ox.
Gọi A’ đối xứng với A qua Ox \( \Rightarrow A'\left( {1; - 2} \right)\) và \(MA = MA'\).
Ta có : \(MA + MB = MA' + MB \ge A'B\). Dấu "=" xảy ra \( \Leftrightarrow M = Ox \cap A'B\).
Phương trình A’B là :
\(\dfrac{{x - 1}}{{3 - 1}} = \dfrac{{y + 2}}{{4 + 2}} \Leftrightarrow 3\left( {x - 1} \right) = y + 2 \Leftrightarrow 3x - y - 5 = 0\)
Cho \(y = 0 \Leftrightarrow x = \dfrac{5}{3} \Rightarrow M\left( {\dfrac{5}{3};0} \right)\)
\( \Rightarrow a = 5;\,\,b = 3 \Rightarrow S = 8\)
Chọn B.