Câu hỏi
(A 2009). Cho đường tròn \(\left( C \right):{x^2} + {y^2} + 4x + 4y + 6 = 0;\,\,\left( \Delta \right):x + my - 2m+3= 0\) . Tìm m để \(\left( \Delta \right)\) cắt (C) tại A, B sao cho diện tích tam giác AIB lớn nhất.
- A \(\left[ \begin{array}{l}m = 0\\m = 1\end{array} \right.\)
- B \(\left[ \begin{array}{l}m = 1\\m = \frac{2}{3}\end{array} \right.\)
- C \(\left[ \begin{array}{l}m = 0\\m = \frac{8}{{15}}\end{array} \right.\)
- D \(\left[ \begin{array}{l}m = 1\\m = \frac{8}{{15}}\end{array} \right.\)
Lời giải chi tiết:
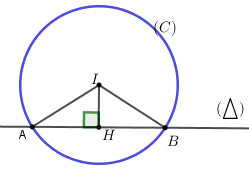
+) Ta có: \(I\left( { - 2; - 2} \right);R = \sqrt {4 + 4 - 6} = \sqrt 2 \)
+) Vẽ \(IH \bot AB\) Khi đó H là trung điểm của AB (quan hệ vuông góc giữa đường kính và dây cung).
+) \({S_{ABI}} = \frac{1}{2}IH.AB = IH.HA\)
+) Tam giác vuông IAH vuông tại H ta có: \(I{H^2} + H{A^2} = I{A^2} = 2\)
Theo Cosi ta có: \(\frac{{I{H^2} + H{A^2}}}{2} \ge \sqrt {I{H^2}.H{A^2}} \Rightarrow IH.HA \le 1 \Rightarrow {S_{ABI\,\,\max }} = 1 \Leftrightarrow IH = HA = 1\) (IH =1 <R thỏa mãn điều kiện)
+) \(d\left( {I,\Delta } \right) = 1 \Leftrightarrow \frac{{\left| { - 2 - 2m - 2m + 3} \right|}}{{\sqrt {1 + {m^2}} }} = 1 \Leftrightarrow \left| { - 4m + 1} \right| = \sqrt {1 + {m^2}} \)
\( \Leftrightarrow 16{m^2} - 8m + 1 = 1 + {m^2} \Leftrightarrow 15{m^2} - 8m = 0 \Leftrightarrow \left[ \begin{array}{l}
m = 0\\
m = \frac{8}{{15}}
\end{array} \right.\)
Vậy \(\left[ \begin{array}{l}m = 0\\m = \frac{8}{{15}}\end{array} \right.\) thỏa mãn yêu cầu bài toán.
Chọn C.







