Câu hỏi
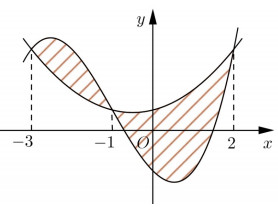
Cho hai hàm số \(f\left( x \right) = a{x^3} + b{x^2} + cx - 1\) và \(g\left( x \right) = d{x^2} + ex + \frac{1}{2}\,\,\left( {a,b,c,d,e \in R} \right)\). Biết rằng đồ thị của hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) cắt nhau tại ba điểm có hoành độ lần lượt là \( - 3; - 1;2\) (tham khảo hình vẽ). Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng
- A \(\dfrac{{253}}{{12}}\)
- B \(\dfrac{{125}}{{12}}\)
- C \(\dfrac{{253}}{{48}}\)
- D \(\dfrac{{125}}{{48}}\)
Phương pháp giải:
Diện tích hình phẳng giới hạn bởi các đường \(y = f\left( x \right);\,\,y = g\left( x \right);\,\,x = a;\,\,x = b\) là \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \)
Lời giải chi tiết:
Xét phương trình hoành độ giao điểm
\(\begin{array}{l}a{x^3} + b{x^2} + cx - 1 = d{x^2} + ex + \dfrac{1}{2}\\ \Leftrightarrow a{x^3} + \left( {b - d} \right){x^2} + \left( {c - e} \right)x - \dfrac{3}{2} = 0\end{array}\)
Dễ thấy phương trình trên có 3 nghiệm phân biệt \( - 3; - 1;2\) nên
\(\begin{array}{l} \Leftrightarrow a{x^3} + \left( {b - d} \right){x^2} + \left( {c - e} \right)x - \dfrac{3}{2} = a\left( {x + 3} \right)\left( {x + 1} \right)\left( {x - 2} \right)\\ \Leftrightarrow a{x^3} + \left( {b - d} \right){x^2} + \left( {c - e} \right)x - \dfrac{3}{2} = a{x^3} + 2a{x^2} - 5ax + 6a\end{array}\)
Đồng nhất hệ số ta được:
\( - \dfrac{3}{2} = 6a \Leftrightarrow a = - \dfrac{1}{4} \Rightarrow f\left( x \right) - g\left( x \right) = - \dfrac{1}{4}\left( {x + 3} \right)\left( {x + 1} \right)\left( {x - 2} \right)\)
\(\begin{array}{l} \Rightarrow S = \int\limits_{ - 3}^{ - 1} {\left| { - \dfrac{1}{4}\left( {x + 3} \right)\left( {x + 1} \right)\left( {x - 2} \right)} \right|dx} + \int\limits_{ - 1}^2 {\left| { - \dfrac{1}{4}\left( {x + 3} \right)\left( {x + 1} \right)\left( {x - 2} \right)} \right|dx} \\\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{4}.\dfrac{{16}}{3} + \dfrac{1}{4}.\dfrac{{63}}{4} = \dfrac{{253}}{{48}}\end{array}\)
Chọn C.







