Câu hỏi
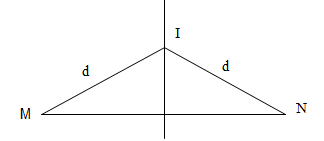
Trên mặt nước, tại M và N có hai nguồn sóng kết hợp dao động ngược pha nhau. Một phần tử nước nằm trên đường trung trực của MN sẽ dao động với biên độ bằng
- A tổng biên độ của hai nguồn
- B hiệu bình phương hai biên độ của hai nguồn
- C tổng bình phương hai biên độ của hai nguồn
- D hiệu biên độ của hai nguồn
Phương pháp giải:
uI = uMI + uNI
Lời giải chi tiết:
Giả sử phương trình sóng tại M và N là:
\(\left\{ \matrix{
{u_M} = {A_1}c{\rm{os}}\omega t \hfill \cr
{u_N} = {A_2}c{\rm{os}}\left( {\omega t + \pi } \right) = - {A_2}c{\rm{os}}\omega t \hfill \cr} \right.\)
Phương trình sóng truyền từ M đến I và từ N đến I:
\(\left\{ \matrix{
{u_{MI}} = {A_1}c{\rm{os}}\left( {\omega t - {{2\pi d} \over \lambda }} \right) \hfill \cr
{u_{NI}} = - {A_2}c{\rm{os}}\left( {\omega t - {{2\pi d} \over \lambda }} \right) \hfill \cr} \right.\)
Phương trình sóng tổng hợp tại I:
\(\eqalign{
& {u_I} = {u_{MI}} + {u_{NI}} = A\cos \omega t = {A_1}c{\rm{os}}\left( {\omega t - {{2\pi d} \over \lambda }} \right) - {A_2}c{\rm{os}}\left( {\omega t - {{2\pi d} \over \lambda }} \right) = \left( {{A_1} - {A_2}} \right)c{\rm{os}}\left( {\omega t - {{2\pi d} \over \lambda }} \right) \cr
& \Rightarrow A = \left| {{A_1} - {A_2}} \right| \cr} \)