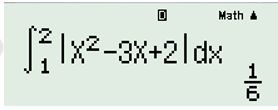Câu hỏi
Tính diện tích S của hình phẳng giới hạn bởi đường thẳng \(y=2x+1\) và đồ thị hàm số \(y={{x}^{2}}-x+3\)
- A
\(S=\frac{1}{7}\) - B \(S=\frac{1}{8}\)
- C \(S=\frac{1}{6}\)
- D \(S=-\frac{1}{6}\)
Phương pháp giải:
Xét phương trình hoành độ giao điểm suy ra các nghiệm \(x=a;\,\,x=b\) , khi đó diện tích cần tính là \(S=\int\limits_{a}^{b}{\left| f\left( x \right)-g\left( x \right) \right|dx}\) .
Lời giải chi tiết:
Xét phương trình hoành độ giao điểm:\(2x+1={{x}^{2}}-x+3\Leftrightarrow {{x}^{2}}-3x+2=0\Leftrightarrow \left[ \begin{align} & x=1 \\ & x=2 \\ \end{align} \right.\)
\(\Rightarrow S=\int\limits_{1}^{2}{\left| {{x}^{2}}-x+3-2x-1 \right|dx}=\int\limits_{1}^{2}{\left| {{x}^{2}}-3x+2 \right|dx}\), sử dụng MTCT ta có:
Vậy \(S=\frac{1}{6}.\)
Chọn C.
Câu hỏi trước
