Câu hỏi
Trong thí nghiệm giao thoa sóng trên mặt nước, hai nguồn S1, S2 cách nhau 20cm dao động theo phương thẳng đứng với các phương trình u1 = u2 = Acos(ωt). Bước sóng trên mặt nước do hai nguồn này tạo ra là λ = 4cm. Trên mặt nước, xét một vân giao thoa cực đại gần đường trung trực của S1S2 nhất; số điểm dao động cùng pha với S1,S2 nằm trên vân này và thuộc hình tròn đường kính S1S2 là
- A 5
- B 4
- C 3
- D 6
Phương pháp giải:
Phương pháp : áp dụng điều kiện để một điểm dao động cực đại và cùng pha với nguồn
Lời giải chi tiết:
Đáp án C
+ Điều kiện để một điểm M dao động cực đại và cùng pha với nguồn:
\(\left\{ \matrix{
{{\rm{d}}_2} - {d_1} = k\lambda \hfill \cr
{d_2} + {d_1} = n\lambda \hfill \cr} \right.\) với k và n cùng chẵn hoặc cùng lẽ.
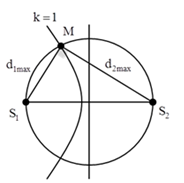
+ M gần trung trực nhất -> k= 1, để M nằm trong nửa đường tròn thì \({{\rm{S}}_1}{S_2} \le {d_1} + {d_2} \le {d_{1\max }} + {d_{2\max }}\,\,\,\left( 1 \right)\).
+ Với
\(\left\{ \matrix{
{{\rm{d}}_{2\max }} - {d_{1\max }} = 4 \hfill \cr
d_{2\max }^2 + d_{1\max }^2 = {20^2} \hfill \cr} \right. \Rightarrow \left\{ \matrix{
{d_{1\max }} = 12 \hfill \cr
{d_{2\max }} = 16 \hfill \cr} \right.\,cm.\)
+ Thay vào (1), ta tìm được \(5 \le n \le 7\), chọn 5, 7 ( cùng lẻ vì ), vớin = 5 ứng với điểm nằm trên trong đường tròn \({{\rm{S}}_1}{S_2} \to \)có 3 điểm cực đại, cùng pha với nguồn và nằm trên dãy k = 1