Câu hỏi
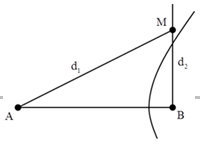
Tại hai điểm A, B cách nhau 13cm trên mặt nước có hai nguồn phát sóng giống nhau. Cùng dao động theo phương trình uA=uB=acos ωt(cm) . Sóng truyền đi trên mặt nước có bước sóng là 2cm, coi biên độ sóng không đổi khi truyền đi. Xét điểm M trên mặt nước thuộc đường thẳng By vuông góc với AB và cách A một khoảng 20cm. Trên By, điểm dao động với biên độ cực đại cách M một khoảng nhỏ nhất bằng
- A 3,14cm.
- B 2,33cm.
- C 2,93cm.
- D 4,11cm.
Lời giải chi tiết:
Đáp án D
+ Xét tỉ số \({{AM - \sqrt {A{M^2} - A{B^2}} } \over \lambda } = 2 \to \) N cực đại gần M nhất khi N thuộc cực đại thứ hoặc
+ Với k =3, ta có:
\(\left\{ \matrix{
{d_1} - {d_2} = 6 \hfill \cr
d_1^2 = d_2^2 + {13^2} \hfill \cr} \right. \Rightarrow \sqrt {d_2^2 + {{13}^2}} - {d_2} = 6 \Rightarrow {d_2} = 11,083\,\,cm.\)
\( \to MN = 4,115\,\,cm.\)
+ Với k = 2, ta có:
\(\left\{ \matrix{
{{\rm{d}}_1} - {d_2} = 4 \hfill \cr
d_1^2 = d_2^2 + {13^2} \hfill \cr} \right. \Rightarrow \sqrt {d_2^2 + {{13}^2}} - {d_2} = 4 \Rightarrow {d_2} = 3,058\,\,cm.\)
\( \to MN = 12,14\,\,cm.\)