Câu hỏi
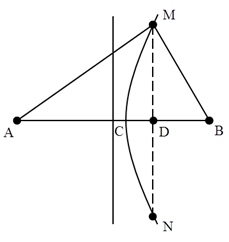
Tại 2 điểm A, B cách nhau 13cm trên mặt nước có 2 nguồn sóng đồng bộ, tạo ra sóng mặt nước có bước sóng là 1,2 cm. M là điểm trên mặt nước cách A và B lần lượt là 12 cm và 5 cm. N đối xứng với M qua AB. Số hyperbol cực đại cắt đoạn MN là:
- A 0
- B 3
- C 2
- D 4
Lời giải chi tiết:
Đáp án C
+ Số đường hyperbol cực đại cắt MN bằng số điểm cực đại trên CD
Ta có : AM – BM = AC – BC = 7 cm.
Và AC + BC = AB = 13 cm → AC = 10 cm.
+ Kết hợp với $$A{M_2} - AD + 2 = B{M_2} - D{B_2}$$
Và DB = AB – AD → AD = 11,08 cm.
+ Xét một điểm bất kỳ trên AB, điều kiện để điểm đó cực đại là:
$$\left\{ \matrix{ {d_2} - {d_1} = k\lambda \hfill \cr {d_2} + {d_1} = AB \Rightarrow {d_2} = {{\left( {AB + k\lambda } \right)} \over 2} \hfill \cr} \right.$$
+ Số điểm cực đại trên AC:$$0 \le {d_2} \le AC \Leftrightarrow 0 \le {{AB + k\lambda } \over 2} \le AC \Leftrightarrow - {{AB} \over \lambda } \le k \le {{2AC - AB} \over \lambda }$$
$$ \Rightarrow - 10,8 \le k \le 5,8$$ → có 16 điểm cực đại.
+ Số điểm cực đại trên AD:
$$0 \le {d_2} \le AD \Rightarrow 0 \le {{AB + k\lambda } \over 2} \le AD \Rightarrow - {{AB} \over \lambda } \le k \le {{2AD - AB} \over \lambda }$$
có 18 điểm cực đại.
Vậy trên CD có 18 – 16 = 2 cực đại, suy ra có 2 đường hyperbol cực đại cắt MN