Câu hỏi
Trong thí nghiệm giao thoa trên mặt nước, hai nguồn sóng kết hợp A và B dao động cùng pha, cùng tần số, cách nhau AB = 8cm tạo ra hai sóng kết hợp có bước sóng λ = 2cm. Một đường thẳng (∆) song song với AB và cách AB một khoảng là 2cm, cắt đường trung trực của AB tại điểm C. Khoảng cách ngắn nhất từ C đến điểm dao động với biên độ cực tiểu trên (∆) là:
- A 0,64cm
- B 0,56cm
- C 0,43cm
- D 0,5cm
Phương pháp giải:
Điều kiện có cực tiểu giao thoa trong giao thoa sóng hai nguồn cùng pha :
\({d_2} - {d_1} = \left( {k + {1 \over 2}} \right)\lambda \)
Lời giải chi tiết:
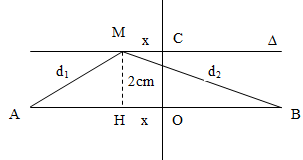
Gọi M là điểm dao động với biên độ cực tiểu gần C nhất trên (∆)
Khoảng cách từ M đến C là : x
Từ hình vẽ ta có :
\(\left\{ \matrix{ {d_1} = \sqrt {4 + {{(4 - x)}^2}} \hfill \cr {d_2} = \sqrt {4 + {{(4 + x)}^2}} \hfill \cr} \right.\)
M là điểm dao động với biên độ cực tiểu gần C nhất nên : d2 – d1 = λ/2 = 1
\(\eqalign{ & \Leftrightarrow \sqrt {{{\left( {4 + x} \right)}^2} + 4} - \sqrt {{{\left( {4 - x} \right)}^2} + 4} = 1 \Leftrightarrow \sqrt {{{\left( {4 + x} \right)}^2} + 4} = 1 + \sqrt {{{\left( {4 - x} \right)}^2} + 4} \Leftrightarrow {\left( {\sqrt {{{\left( {4 + x} \right)}^2} + 4} } \right)^2} = {\left( {1 + \sqrt {{{\left( {4 - x} \right)}^2} + 4} } \right)^2} \cr & \Rightarrow x = 0,56cm \cr} \)
=> Khoảng cách ngắn nhất từ C đến điểm dao động với biên độ cực tiểu trên (∆) là 0,56cm
Chọn B