Phương pháp giải:

- Tính \(y'\), tìm các nghiệm của \(y'\).

- Hàm số đồng biến trên \(\left( {a;b} \right)\) nếu \(y' > 0,\forall x \in \left( {a;b} \right)\).

Lời giải chi tiết:

Ta có:

\(y' = 3{{\rm{x}}^2} - 6{\rm{x}} = 3{\rm{x}}\left( {x - 2} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right.\)

Bảng biến thiên

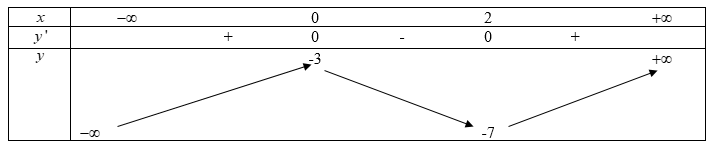
Từ bảng biến thiên ta có hàm số đồng biến trên khoảng\(\left( {2; + \infty } \right)\)

Đáp án C