Câu hỏi
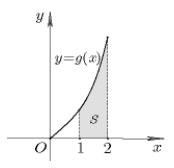
Cho hàm số \(y = f\left( x \right)\) liên tục trên R và hàm số \(y = g\left( x \right) = x.f\left( {{x^2}} \right)\) có đồ thị trên đoạn \(\left[ {0;2} \right]\) như hình vẽ bên. Biết diện tích miền được tô màu là \(S = {5 \over 8},\) tính tích phân \(I = \int\limits_1^4 {f\left( x \right){\rm{d}}x} .\)
- A \(I = {5 \over 4}.\)
- B \(I = {5 \over 2}.\)
- C \(I = 5.\)
- D \(I = 10.\)
Phương pháp giải:
Dựa vào hình vẽ suy ra diện tích hình phẳng tô đậm theo g(x).
Sử dụng phương pháp đổi biến để tính tích phân I.
Lời giải chi tiết:
Dựa vào hình vẽ, ta thấy rằng \(S = \int\limits_1^2 {\left| {g\left( x \right)} \right|{\rm{d}}x} \) vì \(g\left( x \right) \ge 0,\,\,\forall x \in \left[ {1;2} \right] \Rightarrow S = \int\limits_1^2 {g\left( x \right){\rm{d}}x} = {5 \over 8}\)
Khi đó \(S = \int\limits_1^2 {x.f\left( {{x^2}} \right){\rm{d}}x} .\) Đặt \(t = {x^2} \Leftrightarrow {\rm{d}}t = 2x\,{\rm{d}}x \Leftrightarrow x\,{\rm{d}}x = {{{\rm{d}}t} \over 2}\) và đổi cận \(\left\{ \matrix{ x = 1\,\, \Rightarrow \,\,t = 1 \hfill \cr x = 2\,\, \Rightarrow \,\,t = 4 \hfill \cr} \right..\)
Vậy \(S = {5 \over 8} \Leftrightarrow \int\limits_1^4 {{1 \over 2}.f\left( t \right){\rm{d}}t} = {5 \over 8} \Leftrightarrow {1 \over 2}.\int\limits_1^4 {f\left( t \right){\rm{d}}t} = {5 \over 8} \Leftrightarrow \int\limits_1^4 {f\left( x \right){\rm{d}}x} = {5 \over 4}\,\,\buildrel {} \over \longrightarrow \,I = {5 \over 4}.\)
Chọn A.







