Câu hỏi
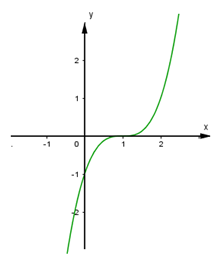
Cho hàm số \(y=f\left( x \right)\) có đồ thị \(\left( C \right)\) như hình vẽ. Hỏi \(\left( C \right)\) là đồ thị của hàm số nào?
- A \(y={{x}^{3}}+1.\)
- B \(y={{\left( x-1 \right)}^{3}}.\)
- C \(y={{\left( x+1 \right)}^{3}}.\)
- D \(y={{x}^{3}}-1.\)
Phương pháp giải:
Phương pháp. Dùng kết quả nếu đồ thị hàm số \(y=f\left( x \right)\) đi qua điểm \(\left( a,b \right)\) thì \(b=f\left( a \right)\) và tính đối xứng của đồ thị để loại trừ các trường hợp không xảy ra.
Lời giải chi tiết:
Lời giải chi tiết.
Từ đồ thị ta quan sát thấy \(y\left( 0 \right)=-1,y\left( 1 \right)=0\) do đó loại A và C.
Hàm số bậc ba nhận nghiệm của phương trình y’’=0 làm tâm đối xứng. Đồ thị đối xứng qua điểm A (1; 0) nên phương trình y’’=0 có nghiệm x = 1.
Đáp án D ta có: \(y'=3{{x}^{2}}\Rightarrow y''=6x=0\Leftrightarrow x=0\ne 1\Rightarrow \)D sai
Do đó chỉ có hàm số \(y={{\left( x-1 \right)}^{3}}\) thỏa mãn.
Chọn đáp án B.