Câu hỏi
Hàm số nào trong bốn hàm số sau có bảng biến thiên như hình vẽ bên?
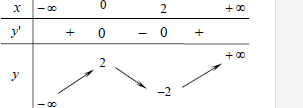
- A \(y = - {x^3} + 3{x^2} - 1.\)
- B \(y = {x^3} + 3{x^2} - 1.\)
- C \(y = {x^3} - 3{x} +2.\)
- D \(y = {x^3} - 3{x^2} + 2.\)
Phương pháp giải:
Phương pháp. Quan sát đồ thị ta thấyhàm số đã cho đồng biến trên \(\left( { - \infty ;0} \right),\,\,\left( {2; + \infty } \right)\) nghịch biến trên \(\left( {0;2} \right)\) và tìm các điểm cực trị để loại các phương án sai.
Lời giải chi tiết:
Quan sát bảng biến thiên ta thấy \(\mathop {\lim }\limits_{x \to - \infty } y = - \infty ,\mathop {\lim }\limits_{x \to + \infty } y = + \infty \,\,\left( 1 \right),\) và hàm số đã cho đồng biến trên \(\left( { - \infty ;0} \right),\,\,\left( {2; + \infty } \right)\) nghịch biến trên\(\left( {0;2} \right)\)
Từ \(1\) ta loại đáp án A.
Xét hàm số \(y = {x^3} + 3{x^2} - 1.\) Ta có \(y' = 3{x^2} + 6x.\) Do đó \(y' = 0 \Leftrightarrow 3{x^2} + 6x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = - 2\end{array} \right..\) Trong trường hợp này các điểm cực trị của hàm số là \(- 2;0\) do đó đáp án B cũng bị loại.
Xét hàm số Ta có Do đó Trong trường hợp này các điểm cực trị của hàm số là do đó đáp án B cũng bị loại.
Xét hàm số \(y = {x^3} + 3{x^2} +2.\)Ta có \(y' = 3{x^2} - 6x.\) Do đó \(y' = 0 \Leftrightarrow 3{x^2} - 6x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right..\)
Ta tính đạo hàm cấp 2. \(y'' = 6x - 6.\) Ta có \(y''\left( 0 \right) = - 6 < 0\) nên \(x=0\) là điểm cực đại của hàm số. Hơn nữa ta co \(y\left( 0 \right) = 2.\)
\(y''\left( 2 \right) = 6.2 - 6 = 6 > 0\) nên \(x=2\) là điểm cực tiểu của hàm số. Hơn nữa ta có \(y\left( 2 \right) = - 2.\)
Chọn đáp án D.







