Câu hỏi
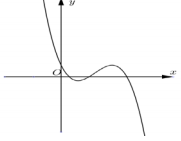
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình vẽ. Mệnh đề nào sau đây đúng?
- A \(a < 0,b > 0,c > 0,d > 0\)
- B \(a > 0,b > 0,c < 0,d > 0\)
- C \(a < 0,b < 0,c < 0,d > 0\)
- D \(a < 0,b > 0,c < 0,{\text{ }}d > 0\)
Phương pháp giải:
Phương pháp:
Quan sát đồ thị, xét các đặc điểm của đồ thị: cắt \(Ox,Oy\), cực đại, cực tiểu,…từ đó suy ra điều kiện \(a,b,c,d\).
Lời giải chi tiết:
Cách giải:
Vì \(y \to -\infty \) khi \(x \to + \infty \) nên \(a < 0\)
Đồ thị hàm số cắt \(Oy\) tại điểm có tung độ dương \( \Rightarrow d > 0\)
Có \(y' = 3a{x^2} + 2bx + c = 0\) có \(2\) nghiệm dương (\(2\) điểm cực trị của đồ thị hàm số có hoành độ dương) \( \Rightarrow b\) trái dấu với \(a\) và \(c\) cùng dấu với \(a\)
\( \Rightarrow b > 0\) và \(c < 0\)
Chọn đáp án D
Câu hỏi trước
