Câu hỏi
Một con lắc lò xo gồm quả cầu khối lượng m = 100 (g) treo vào một lò xo có độ cứng k = 20 N/m. Kéo quả cầu thẳng đứng xuống dưới vị trí cân bằng một đoạn 2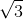 cm rồi thả cho quả cầu trở về vị trí cân bằng với vận tốc có độ lớn là 0,2
cm rồi thả cho quả cầu trở về vị trí cân bằng với vận tốc có độ lớn là 0,2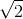 m/s. Chọn gốc thời gian là lúc thả quả cầu, trục Ox hướng xuống dưới, gốc toạ độ O tại vị trí cân bằng của quả cầu. Cho g = 10 m/s2. Phương trình dao động của quả cầu có dạng là
m/s. Chọn gốc thời gian là lúc thả quả cầu, trục Ox hướng xuống dưới, gốc toạ độ O tại vị trí cân bằng của quả cầu. Cho g = 10 m/s2. Phương trình dao động của quả cầu có dạng là
- A x = 4 sin(10
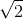 t + π/4) cm.
t + π/4) cm. - B x = 4sin(10
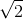 t + 2π/3)cm.
t + 2π/3)cm.
- C x = 4 sin(10
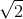 + 5π/6) cm.
+ 5π/6) cm. - D x = 4sin(10
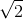 t + π/3)cm.
t + π/3)cm.
Phương pháp giải:
Sử dụng lí thuyết về PT dao động \(x = A\cos \left( {\omega t + \varphi } \right)\) , trong đó A là biên độ dao động, ω là tốc độ góc, φ là pha dao động tại thời điểm ban đầu; lí thuyết về dao động điều hòa của CLLX thẳng đứng
Lời giải chi tiết:
* Tần số góc của CLLX \(\omega = \sqrt {{k \over m}} = \sqrt {{{20} \over {0,1}} = } 10\sqrt 2 rad/s\)
*Kéo quả cầu thẳng đứng xuống dưới vị trí cân bằng một đoạn 2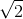 cm rồi thả cho quả cầu trở về vị trí cân bằng với vận tốc có độ lớn là 0,2
cm rồi thả cho quả cầu trở về vị trí cân bằng với vận tốc có độ lớn là 0,2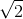 m/s = 20
m/s = 20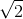 cm/s.
cm/s.
=> Biên độ \(A = \sqrt {{x^2} + {{{v^2}} \over {{\omega ^2}}}} = \sqrt {{2^2}.3 + {{{{20}^2}.2} \over {{{10}^2}.2}}} = 4cm\)
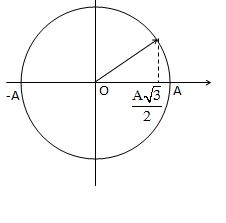
* Gốc thời gian là lúc thả quả cầu, nghĩa là lúc vật có li độ x = 2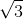 cm và chuyển động theo chiều âm(vì chiều dương hướng xuống)
cm và chuyển động theo chiều âm(vì chiều dương hướng xuống)
=> Pha ban đầu φ = π/6 rad
Vậy, PT dao động của vật là \(x = 4\cos \left( {10\sqrt 2 t + {\pi \over 6}} \right)cm = 4\sin \left( {10\sqrt 2 t + {{2\pi } \over 3}} \right)cm\)
=> Chọn đáp án B