Câu hỏi
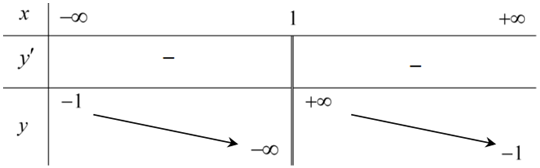
Bảng biến thiên trong hình dưới là đồ thị của một số hàm số trong bốn hàm số được liệt kê ở bốn đáp án dưới đây. Hỏi hàm số đó là hàm số nào?
- A \(y = \dfrac{{ - x - 3}}{{x - 1}}\)
- B \(y = \dfrac{{x + 3}}{{x - 1}}\)
- C \(y = \dfrac{{ - x + 3}}{{x - 1}}\)
- D \(y = \dfrac{{ - x - 2}}{{x - 1}}\)
Phương pháp giải:
Dựa vào BBT, nhận xét các đường tiệm cận của đồ thị hàm số và tính đơn điệu của hàm số để chọn đáp án đúng.
Lời giải chi tiết:
Dựa vào BBT ta thấy đồ thị hàm có TCĐ là \(x = 1\) và TCN là \(y = - 1\)
\( \Rightarrow \) Loại đáp án B.
Hàm số đã cho là hàm số nghịch biến.
+) Xét đáp án A: \(y = \dfrac{{ - x + 3}}{{x - 1}}\) có \(y' = \dfrac{{1 + 3}}{{{{\left( {x - 1} \right)}^2}}} = \dfrac{4}{{{{\left( {x - 1} \right)}^2}}} > 0\)
\( \Rightarrow \) Hàm số đã cho đồng biến trên từng khoảng xác định \( \Rightarrow \) Loại đáp án A.
+) Xét đáp án C: \(y = \dfrac{{ - x + 3}}{{x - 1}}\) có \(y' = \dfrac{{1 - 3}}{{{{\left( {x - 1} \right)}^2}}} = \dfrac{{ - 2}}{{{{\left( {x - 1} \right)}^2}}} < 0\)
\( \Rightarrow \) Hàm số đã cho nghịch biến trên từng khoảng xác định \( \Rightarrow \) Loại đáp án C.
Chọn C.