Câu hỏi
Cho đồ thị hàm số \(y = a{x^4} + b{x^2} + c\) có đồ thị như sau:
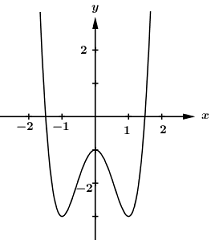
Xác định dấu của \(a;\,\,b;\,\,c.\)
- A \(a > 0,\,\,b > 0,\,\,c > 0.\)
- B \(a > 0,\,\,b < 0,\,\,c < 0.\)
- C \(a > 0,\,\,b < 0,\,\,c > 0.\)
- D \(a < 0,\,\,b > 0,\,\,c < 0.\)
Phương pháp giải:
- Dựa vào nét cuối cùng của đồ thị hàm số suy ra dấu của hệ số \(a\).
- Dựa vào giao điểm của đồ thị hàm số với trục tung suy ra dấu của hệ số \(c\).
- Dựa vào số điểm cực trị của hàm số:
+ Hàm số có 3 điểm cực trị thì \(ab < 0\).
+ Hàm số có 1 điểm cực trị thì \(ab > 0\).
Lời giải chi tiết:
- Nét cuối cùng của đồ thị hàm số đi lên \( \Rightarrow a > 0\).
- Đồ thị hàm số cắt trục tung tại điểm có hoành độ âm nên \(c < 0\).
- Đồ thị hàm số có 3 điểm cực trị nên \(ab < 0\), mà \(a > 0\) nên \(b < 0\).
Vậy \(a > 0,\,\,b < 0,\,\,c < 0\).
Chọn B.







