Câu hỏi
Cho khối chóp \(S.ABCD\) có \(ABCD\) là hình chữ nhật, \(AD = 2a\), \(AB = a\). Gọi \(H\) là trung điểm của \(AD\), biết \(SH\) vuông góc với mặt phẳng đáy. Tính thể tích khối chóp \(S.ABCD\) biết \(SA = a\sqrt 5 \).
- A \({a^3}\)
- B \(\dfrac{{{a^3}}}{3}\)
- C \(\dfrac{{4{a^3}}}{3}\)
- D \(\dfrac{{2{a^3}}}{3}\)
Phương pháp giải:
- Áp dụng định lí Pytago trong tam giác vuông tính chiều cao \(AH\).
- Tính thể tích khối chóp \(V = \dfrac{1}{3}SH.{S_{ABCD}}\).
Lời giải chi tiết:
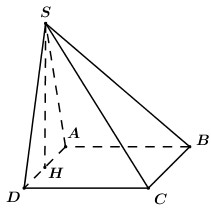
Ta có: \(AH = \dfrac{{AD}}{2} = a\).
Áp dụng định lí Pytago trong tam giác vuông \(SAH\) có:
\(SH = \sqrt {S{A^2} - A{H^2}} = \sqrt {5{a^2} - {a^2}} = 2a\).
\({S_{ABCD}} = AB.AD = a.2a = 2{a^2}\) .
Vậy \({V_{S.ABCD}} = \dfrac{1}{3}SH.{S_{ABCD}} = \dfrac{1}{3}.2a.2{a^2} = \dfrac{{4{a^3}}}{3}\).
Chọn C.
Câu hỏi trước
