Câu hỏi
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\). Gọi \(M\) và \(N\) lần lượt là trung điểm của các cạnh \(AB\) và \(AD\); \(H\) là giao điểm của \(CN\) và \(DM\). Biết \(SH\) vuông góc với mặt phẳng \(\left( {ABCD} \right)\) và \(SH = a\sqrt 3 \). Tính thể tích khối chóp \(S.CDNM\)?
- A \(V = \dfrac{{5{a^3}\sqrt 3 }}{8}\)
- B \(V = \dfrac{{5{a^3}\sqrt 3 }}{{24}}\)
- C \(V = \dfrac{{5{a^3}}}{8}\)
- D \(V = \dfrac{{5{a^3}\sqrt 3 }}{{12}}\)
Phương pháp giải:
- Tính diện tích tứ giác \(CDNM\): \({S_{CDNM}} = {S_{ABCD}} - {S_{\Delta AMN}} - {S_{\Delta BCM}}\).
- Tính thể tích khối chóp \(V = \dfrac{1}{3}SH.{S_{CDNM}}\).
Lời giải chi tiết:
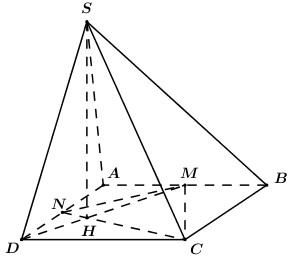
Ta có:
\(\begin{array}{l}{S_{\Delta AMN}} = \dfrac{1}{2}AM.AN = \dfrac{1}{2}.\dfrac{a}{2}.\dfrac{a}{2} = \dfrac{{{a^2}}}{8}\\{S_{\Delta BCM}} = \dfrac{1}{2}BC.BM = \dfrac{1}{2}.a.\dfrac{a}{2} = \dfrac{{{a^2}}}{4}\\{S_{ABCD}} = A{B^2} = {a^2}\\ \Rightarrow {S_{CDNM}} = {S_{ABCD}} - {S_{\Delta AMN}} - {S_{\Delta BCM}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {a^2} - \dfrac{{{a^2}}}{8} - \dfrac{{{a^2}}}{4} = \dfrac{{5{a^2}}}{8}\end{array}\)
Vậy \({V_{S.CDNM}} = \dfrac{1}{3}SH.{S_{CDNM}} = \dfrac{1}{3}.a\sqrt 3 .\dfrac{{5{a^2}}}{8} = \dfrac{{5{a^3}\sqrt 3 }}{{24}}\).
Chọn B.







