Câu hỏi
Cho khối nón đỉnh \(S\) só độ dài đường sinh là \(a,\) góc giữa đường sinh và mặt đáy là \(60^\circ .\) Thể tích khối nón là
- A \(V = \dfrac{{\pi {a^3}\sqrt 3 }}{{24}}.\)
- B \(V = \dfrac{{\pi {a^3}\sqrt 3 }}{8}.\)
- C \(V = \dfrac{{\pi {a^3}}}{8}.\)
- D \(V = \dfrac{{3\pi {a^3}}}{8}.\)
Phương pháp giải:
- Xác định góc giữa đường sinh và mặt đáy.
- Sử dụng tỉ số lượng giác tính chiều cao và bán kính đáy của hình nón.
- Thể tích khối nón có chiều cao \(h\), bán kính đáy \(r\) là \(V = \dfrac{1}{3}\pi {r^2}h\).
Lời giải chi tiết:
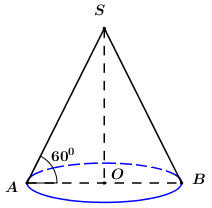
Gọi \(O\) là tâm đáy hình nón và \(SA\) là một đường sinh bất kì \( \Rightarrow SA = l = a\).
Khi đó ta có góc giữa \(SA\) và mặt đáy là \(\angle SAO = {60^0}\).
Xét \(\Delta SAO\) có: \(SO = SA.\sin {60^0} = \dfrac{{a\sqrt 3 }}{2} = h\), \(OA = SA.\cos {60^0} = \dfrac{a}{2} = r\).
Vậy thể tích khối nón là \(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi .{\left( {\dfrac{a}{2}} \right)^2}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{\pi {a^3}\sqrt 3 }}{{24}}\).
Chọn A.







