Phương pháp giải:

- Giả sử thiết diện của hình chóp cắt bởi mặt phẳng đi qua đỉnh và cách tâm một khoảng \(\dfrac{a}{3}\) là tam giác \(SAB\). Gọi \(O\) là tâm đáy của hình nón.

- Xác định khoảng cách từ \(O\) đến \(\left( {SAB} \right)\).

- Sử dụng hệ thức lượng và định lí Pytago trong tam giác vuông tính bán kính đáy của hình nón.

- Thể tích khối nón có chiều cao \(h\), bán kính đáy \(r\) là \(V = \dfrac{1}{3}\pi {r^2}h\).

Lời giải chi tiết:

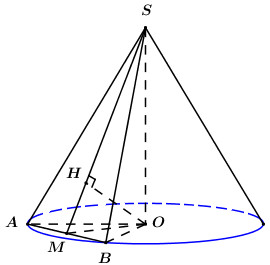
Giả sử thiết diện của hình chóp cắt bởi mặt phẳng đi qua đỉnh và cách tâm một khoảng \(\dfrac{a}{3}\) là tam giác \(SAB\), ta có \(\Delta SAB\) vuông cân tại \(S\).

Gọi \(O\) là tâm đáy của hình nón, gọi \(M\) là trung điểm của \(AB\). Trong \(\left( {SOM} \right)\) kẻ \(OH \bot SM\,\,\left( {H \in SM} \right)\).

Ta có:

\(\begin{array}{l}\left\{ \begin{array}{l}AB \bot OM\\AB \bot SO\end{array} \right. \Rightarrow SB \bot \left( {SOM} \right) \Rightarrow AB \bot OH\\\left\{ \begin{array}{l}OH \bot AB\\OH \bot SM\end{array} \right. \Rightarrow OH \bot \left( {SAB} \right)\\ \Rightarrow d\left( {O;\left( {SAB} \right)} \right) = OH = \dfrac{a}{3}\end{array}\)

Áp dụng hệ thức lượng trong tam giác vuông \(SOM\) ta có:

\(\begin{array}{l}\dfrac{1}{{O{H^2}}} = \dfrac{1}{{S{O^2}}} + \dfrac{1}{{O{M^2}}}\\ \Leftrightarrow \dfrac{9}{{{a^2}}} = \dfrac{1}{{{a^2}}} + \dfrac{1}{{O{M^2}}}\\ \Leftrightarrow \dfrac{1}{{O{M^2}}} = \dfrac{8}{{{a^2}}}\\ \Leftrightarrow OM = \dfrac{{a\sqrt 2 }}{4}\end{array}\)

Lại có \(SM = \dfrac{{SO.OM}}{{OH}} = \dfrac{{a.\dfrac{{a\sqrt 2 }}{4}}}{{\dfrac{a}{3}}} = \dfrac{{3\sqrt 2 a}}{4}\), tam giác \(SAB\) vuông cân tại \(S\) nên \(SM = \dfrac{1}{2}AB\).

\( \Rightarrow AB = 2SM = \dfrac{{3\sqrt 2 a}}{2}\) \( \Rightarrow AM = \dfrac{1}{2}AB = \dfrac{{3\sqrt 2 a}}{4}\).

Áp dụng định lí Pytago trong tam giác vuông \(OAM\) ta có:

\(OA = \sqrt {O{M^2} + A{M^2}}  = \sqrt {{{\left( {\dfrac{{a\sqrt 2 }}{4}} \right)}^2} + {{\left( {\dfrac{{3\sqrt 2 a}}{4}} \right)}^2}}  = \dfrac{{a\sqrt 5 }}{2}\).

Vậy thể tích khối nón là: \(V = \dfrac{1}{3}\pi O{A^2}.SO = \dfrac{1}{3}\pi .{\left( {\dfrac{{a\sqrt 5 }}{2}} \right)^2}.a = \dfrac{{5\pi {a^3}}}{{12}}\).

Chọn A.