Câu hỏi
Cho tứ diện \(OABC\) có \(OA,OB,OC\) đôi một vuông góc với nhau và \(OA = 2a,\,OB = 3a,\,OC = 8a\), \(M\) là trung điểm của đoạn \(OC\). Tính thể tích V của khối tứ diện \(OABM\).
- A \(V = 3{a^3}\).
- B \(V = 4{a^3}\).
- C \(V = 8{a^3}\).
- D \(V = 6{a^3}\).
Phương pháp giải:
Công thức thể tích khối tứ diện vuông với độ dài ba cạnh góc vuông là \(a,b,c\) là: \(V = \dfrac{1}{6}abc\).
Lời giải chi tiết:
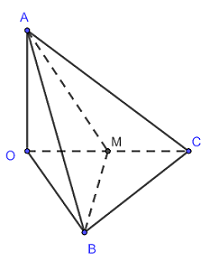
Tứ diện \(OABM\) là tứ diện vuông, có thể tích là:
\(V = \dfrac{1}{6}OA.OB.OM = \dfrac{1}{6}.2a.3a.\dfrac{{8a}}{2} = 4{a^3}\).
Chọn B.
Câu hỏi trước
