Câu hỏi
Cho khối tứ diện \(ABCD\) có cạnh \(AC,BD\) thỏa mãn \(A{C^2} + B{D^2} = 16\) và các cạnh còn lại đều bằng 6. Thể tích khối tứ diện \(ABCD\) đạt giá trị lớn nhất bằng
- A \(\dfrac{{16\sqrt 2 }}{3}\).
- B \(\dfrac{{32\sqrt 2 }}{3}\)
- C \(\dfrac{{16\sqrt 3 }}{3}\).
- D \(\dfrac{{32\sqrt 3 }}{3}\).
Phương pháp giải:
- Gọi E, F lần lượt là trung điểm của BD, AC. Sử dụng định lí Pytago tính BF, EF.
- Tính diện tích tam giác BDF.
- Chứng minh \({V_{ABCD}} = \dfrac{1}{3}.{S_{BDF}}.AC\).
- Áp dụng BĐT: \(ab \le \dfrac{{{a^2} + {b^2}}}{2}\).
Lời giải chi tiết:
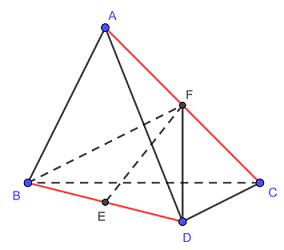
Gọi E, F lần lượt là trung điểm của BD, AC. Giả sử \(AC = a,\,\,\,BD = b\), theo giả thiết ta có: \({a^2} + {b^2} = 16\,\,\left( {a,b > 0} \right)\).
Xét \(\Delta ABC\) và \(\Delta ADC\) có:
AC chung
AB = AD (gt)
BC = CD (gt)
\( \Rightarrow \Delta ABC = \Delta ADC\,\,\left( {c.c.c} \right) \Rightarrow BF = DF\) (2 trung tuyến tương ứng)
\( \Rightarrow \Delta BDF\) cân tại F \( \Rightarrow EF \bot BD\) (đường trung tuyến đồng thời là đường cao).
Ta có: \(BF = \sqrt {A{B^2} - A{F^2}} = \sqrt {{6^2} - {{\left( {\dfrac{a}{2}} \right)}^2}} = \sqrt {36 - \dfrac{{{a^2}}}{4}} \)
\(EF = \sqrt {B{F^2} - B{E^2}} = \sqrt {36 - \dfrac{{{a^2}}}{4} - \dfrac{{{b^2}}}{4}} = \sqrt {36 - \dfrac{{16}}{4}} = \sqrt {32} \)
\( \Rightarrow {S_{BDF}} = \dfrac{1}{2}.EF.BD = \dfrac{1}{2}.\sqrt {32} .b = 2\sqrt 2 b\)
Do \(\left\{ \begin{array}{l}AC \bot BF\\AC \bot DF\end{array} \right. \Rightarrow AC \bot \left( {BDF} \right)\).
Ta có:
\(\begin{array}{l}{V_{ABCD}} = {V_{A.BDF}} + {V_{C.BDF}}\\\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{3}.AF.{S_{BDF}} + \dfrac{1}{3}.CF.{S_{BDF}}\\\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{3}.{S_{BDF}}.\left( {AF + CF} \right)\\\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{3}.{S_{BDF}}.AC\\\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{3}.a.2\sqrt 2 b = \dfrac{{2\sqrt 2 }}{3}ab\end{array}\)
Áp dụng BĐT Cô-si ta có \(ab \le \dfrac{{{a^2} + {b^2}}}{2} = \dfrac{{16}}{2} = 8\).
\( \Rightarrow {V_{ABCD}} \le \dfrac{{2\sqrt 2 }}{3}.8 = \dfrac{{16\sqrt 2 }}{3}\).
Vậy \({V_{\max }} = \dfrac{{16\sqrt 2 }}{3}\) khi và chỉ khi \(\left\{ \begin{array}{l}a = b\\{a^2} + {b^2} = 16\end{array} \right. \Leftrightarrow a = b = 2\sqrt 2 \).
Chọn A.







