Câu hỏi
Cho hình chóp tứ giác đều \(S.ABCD\) có tất cả các cạnh đều bằng a, tâm của đáy là O. Gọi M, N tương ứng là trung điểm của các cạnh SA, SC. Gọi E là giao điểm của SD và mặt phẳng (BMN). Tính thể tích V của khối chóp O.BMEN.
- A \(V = \dfrac{{{a^3}\sqrt 2 }}{{36}}\).
- B \(V = \dfrac{{{a^3}\sqrt 2 }}{{12}}\).
- C \(V = \dfrac{{{a^3}\sqrt 2 }}{{18}}\).
- D \(V = \dfrac{{{a^3}\sqrt 2 }}{{24}}\).
Phương pháp giải:
+) Định lí Menelaus: Cho tam giác ABC. Các điểm D, E, F lần lượt nằm trên các đường thẳng BC, CA, AB. Khi đó D, E, F thẳng hàng khi và chỉ khi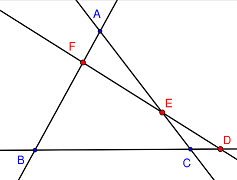
\(\dfrac{{FA}}{{FB}}.\dfrac{{DB}}{{DC}}.\dfrac{{EC}}{{EA}} = 1\){\displaystyle {\frac {\overline {FA}}{\overline {FB}}}\cdot {\frac {\overline {DB}}{\overline {DC}}}\cdot {\frac {\overline {EC}}{\overline {EA}}}=1.}
+) Thể tích hình chóp tứ giác đều \(S.ABCD\) có tất cả các cạnh đều bằng a là:
\(V = \dfrac{{{a^3}\sqrt 2 }}{6}\)
Lời giải chi tiết:
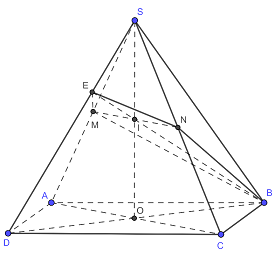
Gọi I là giao điểm của SO và MN. Khi đó, giao điểm E của SD và mặt phẳng (BMN) là giao của ID và SB.
Xét tam giác SOD, có:
\(\dfrac{{ES}}{{ED}}.\dfrac{{BD}}{{BO}}.\dfrac{{IO}}{{IS}} = 1 \Leftrightarrow \dfrac{{ES}}{{ED}}.2.1 = 1 \Leftrightarrow \dfrac{{ES}}{{ED}} = \dfrac{1}{2}\)\( \Rightarrow \dfrac{{SE}}{{SD}} = \dfrac{1}{3}\)
Do I là trung điểm của SO nên \(d\left( {O;\left( {BNEM} \right)} \right) = d\left( {S;\left( {BNEM} \right)} \right)\)\( \Rightarrow {V_{O.BNEM}} = {V_{S.BNEM}}\)
Lại có:
\({V_{S.ENB}} = \dfrac{{SN}}{{SC}}.\dfrac{{SE}}{{SD}}.{V_{S.BDC}} = \dfrac{1}{2}.\dfrac{1}{3}.{V_{S.BDC}} = \dfrac{1}{6}{V_{S.BDC}} = \dfrac{1}{{12}}{V_{S.ABCD}}\) và \({V_{S.EMB}} = \dfrac{1}{{12}}{V_{S.ABCD}}\) \( \Rightarrow {V_{S.BNEM}} = \dfrac{1}{6}{V_{S.ABCD}} = \dfrac{1}{6}.\dfrac{{{a^3}\sqrt 2 }}{6} = \dfrac{{{a^3}\sqrt 2 }}{{36}}\).
Chọn A.







