 Môn Toán - Lớp 12
Môn Toán - Lớp 12
 30 bài tập trắc nghiệm giá trị lớn nhất, giá trị nhỏ nhất của hàm số mức độ thông hiểu
30 bài tập trắc nghiệm giá trị lớn nhất, giá trị nhỏ nhất của hàm số mức độ thông hiểu
Câu hỏi
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = \dfrac{{{x^3}}}{3} + 2{x^2} + 3x - 4\) trên đoạn \(\left[ { - 4;0} \right]\) lần lượt là \(M\) và \(m\). Giá trị của tổng \(M + m\) bằng bao nhiêu?
- A \(M + m = - \dfrac{4}{3}\).
- B \(M + m = \dfrac{4}{3}\).
- C \(M + m = - \dfrac{{28}}{3}\).
- D \(M + m = - 4\).
Phương pháp giải:
- Tìm đạo hàm của hàm số và tìm nghiệm \(y' = 0\).
- Lập bảng biến thiên của hàm số trong khoảng yêu cầu.
- Dựa vào bảng biến thiên để kết luận GTLN, GTNN của hàm số.
Lời giải chi tiết:
Hàm số \(y = \dfrac{{{x^3}}}{3} + 2{x^2} + 3x - 4\) có TXĐ \(D = \mathbb{R}\).
Ta có: \(y' = {x^2} + 4x + 3 = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = - 3\end{array} \right.\)
Bảng biến thiên trên đoạn \(\left[ { - 4;0} \right]\):
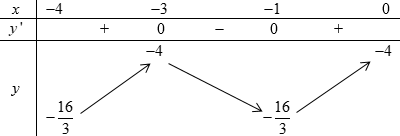
Dựa vào bảng biến thiên ta thấy trên đoạn \(\left[ { - 4;0} \right]\); hàm số có:
Giá trị lớn nhất \(M = - 4\); giá trị nhỏ nhất \(m = - \dfrac{{16}}{3}\).
Vậy \(M + m = - 4 - \dfrac{{16}}{3} = - \dfrac{{28}}{3}.\)
Chọn C.






