Câu hỏi
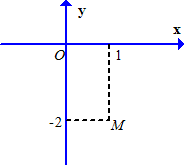
Trên mặt phẳng tọa độ ,điểm \(M\) trong hình vẽ bên là điểm biểu diễn số phức \(z\). Khẳng định nào sau đây là đúng?
- A \(\overline z = 1 - 2i\).
- B \(\left| z \right| = \sqrt 5 \)
- C \(z = 1 + 2i\)
- D \(z = - 2 + i\)
Phương pháp giải:
- Điểm biểu diễn của số phức \(z = a + bi\) là \(M\left( {a;b} \right)\).
- Số phức \(z = a + bi\) có số phức liên hợp \(\bar z = a - bi\).
- Số phức \(z = a + bi\) có môđun \(\left| z \right| = \sqrt {{a^2} + {b^2}} \).
Lời giải chi tiết:
Ta có \(M\left( {1; - 2} \right)\) là điểm biểu phức z nên \(z = 1 - 2i\)
\(\begin{array}{l} \Rightarrow \overline z = 1 + 2i\\\,\,\,\,\,\left| z \right| = \sqrt {{1^2} + {{\left( { - 2} \right)}^2}} = \sqrt 5 .\end{array}\)
Vậy khẳng định B đúng.
Chọn B.
Câu hỏi trước
