Câu hỏi
Quay tam giác ABC vuông tại B với AB = 2; BC = 1 quanh trục AB. Tính thể tích khối tròn xoay thu được:
- A \(\dfrac{{4\sqrt 5 \pi }}{{15}}\)
- B \(\dfrac{{4\sqrt 5 \pi }}{5}\)
- C \(\dfrac{{2\pi }}{3}\)
- D \(\dfrac{{4\pi }}{3}\)
Phương pháp giải:
Thể tích khối nón có chiều cao h, bán kính đáy r là \(V = \dfrac{1}{3}\pi {r^2}h\).
Lời giải chi tiết:
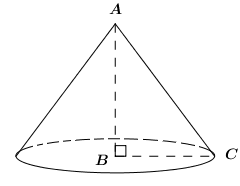
Khi quay tam giác vuông ABC vuông tại B quanh cạnh AB ta nhận được khối nón có chiều cao \(h = AB = 2\), bán kính đáy \(r = BC = 1\).
Vậy thể tích khối nón là: \(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi {.1^2}.2 = \dfrac{{2\pi }}{3}\).
Chọn C.
Câu hỏi trước
