Câu hỏi
Cho hàm số \(f\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right]\) và thỏa mãn \(\int\limits_a^0 {f\left( x \right)dx = m} \), \(\int\limits_0^b {f\left( x \right)dx = n} \). Diện tích hình phẳng trong hình vẽ bằng
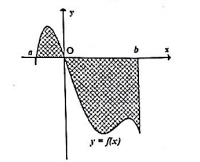
- A \(m.n\)
- B \(m - n\)
- C \(m + n\)
- D \(n - m\)
Phương pháp giải:
Cho hàm số \(f\left( x \right)\)liên tục \(\left[ {a;b} \right]\), diện tích hình phẳng giới hạn bởi đồ thị hàm số \(f\left( x \right)\), các đường thẳng \(x = a,\,\,x = b\) và trục Ox là \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|dx} .\)
Lời giải chi tiết:
Gọi \({S_1}\) là diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục hoành, đường thẳng \(x = a,\,\,x = 0\,\,\left( {a < 0} \right)\), ta có \({S_1} = \int\limits_a^0 {\left| {f\left( x \right)} \right|dx} = \int\limits_a^0 {f\left( x \right)dx} = m\).
Gọi \({S_2}\) là diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục hoành, đường thẳng \(x = 0,\,\,x = b\,\,\left( {b > 0} \right)\), ta có \({S_2} = \int\limits_0^b {\left| {f\left( x \right)} \right|dx} = - \int\limits_0^b {f\left( x \right)dx} = - n\).
Vậy diện tích cần tính là \(S = {S_1} + {S_2} = m - n.\)
Chọn B.







