Câu hỏi
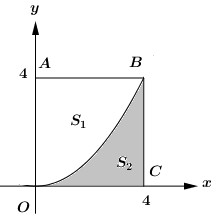
Hình vuông OABC có cạnh bằng 4 được chia thành hai phần bởi đường cong \(\left( C \right)\) có phương trình \(y = \dfrac{1}{4}{x^2}\). Gọi \({S_1};\,\,{S_2}\) lần lượt là diện tích phần không bị gạch và phần bị gạch như hình bên dưới. Tỉ số \(\dfrac{{{S_1}}}{{{S_2}}}\) bằng.
- A \(\dfrac{3}{2}.\)
- B \(3.\)
- C \(\dfrac{1}{2}.\)
- D \(2.\)
Phương pháp giải:
- \({S_2}\) là diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = \dfrac{1}{4}{x^2}\), trục hoành, đường thẳng \(x = 0\) và \(x = 4\).
- Cho hai hàm số \(f\left( x \right);g\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right]\). Diện tích hình phẳng giới hạn bởi đồ thị \(y = f\left( x \right),y = g\left( x \right)\) và các đường thẳng \(x = a,x = b\) bằng \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \).
- Tính \({S_1} = {S_{OABC}} - {S_2}\).
- Tính tỉ số \(\dfrac{{{S_1}}}{{{S_2}}}\).
Lời giải chi tiết:
Ta thấy \({S_2}\) là diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = \dfrac{1}{4}{x^2}\), trục hoành, đường thẳng \(x = 0\) và \(x = 4\) nên \({S_2} = \int\limits_0^4 {\dfrac{1}{4}{x^2}dx} = \dfrac{{16}}{3}.\)
Ta có: \(OABC\) là hình vuông cạnh \(4\) nên \({S_{ABCO}} = {4^2} = 16\).
\( \Rightarrow {S_1} = {S_{OABC}} - {S_2} = 16 - \dfrac{{16}}{3} = \dfrac{{32}}{3}.\)
Vậy \(\dfrac{{{S_1}}}{{{S_2}}} = \dfrac{{32}}{3}:\dfrac{{16}}{3} = 2.\)
Chọn D.







