Câu hỏi
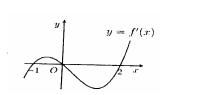
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị hàm số \(y = f'\left( x \right)\) như hình vẽ dưới. mệnh đề nào sau đây là đúng?
- A \(f\left( 0 \right) > f\left( 2 \right) > f\left( { - 1} \right).\)
- B \(f\left( 0 \right) > f\left( { - 1} \right) > f\left( 2 \right).\)
- C \(f\left( 2 \right) > f\left( 0 \right) > f\left( { - 1} \right).\)
- D \(f\left( { - 1} \right) > f\left( 0 \right) > f\left( 2 \right).\)
Phương pháp giải:
- Lập BBT của hàm số \(y = f\left( x \right)\).
- So sánh \(f\left( 0 \right)\) với \(f\left( { - 1} \right),\,\,f\left( 2 \right)\).
- Gọi \({S_1}\) là diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f'\left( x \right)\), đường thẳng \(x = - 1,\,\,x = 0\) và trục hoành, \({S_2}\) là diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f'\left( x \right)\), đường thẳng \(x = 0,\,\,x = 2\) và trục hoành.
- Giải bất phương trình \({S_2} > {S_1}\).
Lời giải chi tiết:
Dựa vào đồ thị hàm số ta có \(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 0\\x = 2\end{array} \right.\)
Bảng biến thiên:
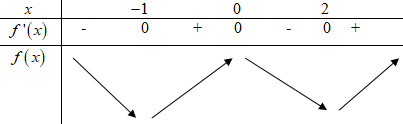
Dựa vào bảng biến thiên ta thấy \(f\left( 0 \right) > f\left( { - 1} \right).\,\,f\left( 0 \right) > f\left( 2 \right)\).
Gọi \({S_1}\) là diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f'\left( x \right)\), đường thẳng \(x = - 1,\,\,x = 0\) và trục hoành, ta có: \({S_1} = \int\limits_{ - 1}^0 {\left| {f'\left( x \right)dx} \right|} = \int\limits_{ - 1}^0 {f'\left( x \right)dx} = f\left( 0 \right) - f\left( { - 1} \right) > 0\).
Gọi \({S_2}\) là diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f'\left( x \right)\), đường thẳng \(x = 0,\,\,x = 2\) và trục hoành, ta có: \({S_2} = \int\limits_0^2 {\left| {f'\left( x \right)dx} \right|} = - \int\limits_0^2 {f'\left( x \right)dx} = - \left[ {f\left( 2 \right) - f\left( 0 \right)} \right] = f\left( 0 \right) - f\left( 2 \right) > 0\).
Dựa vào đồ thị hàm số ta thấy được: \({S_2} > {S_1} \Leftrightarrow f\left( 0 \right) - f\left( 2 \right) > f\left( 0 \right) - f\left( { - 1} \right) \Leftrightarrow f\left( 2 \right) < f\left( { - 1} \right)\).
Vậy \(f\left( 0 \right) > f\left( { - 1} \right) > f\left( 2 \right)\).
Chọn B.







