Câu hỏi
Cho hình thang cong \(\left( H \right)\) giới hạn bởi các đường thẳng \(y = \dfrac{1}{x}\), \(x = \dfrac{1}{2},\,\,x = 2\) và trục hoành. Đường thẳng \(x = k\,\,\left( {\dfrac{1}{2} < k < 2} \right)\) chia \(\left( H \right)\) thành hai phần có diện tích là \({S_1}\) và \({S_2}\) như hình vẽ dưới đây:
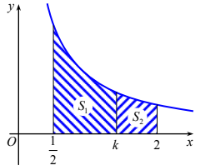
Tìm tất cả các giá trị thực của \(k\) để \({S_1} = 3{S_2}\)
- A \(k = \sqrt 2 \)
- B \(k = 1\)
- C \(k = \dfrac{7}{5}\)
- D \(k = \sqrt 3 \)
Phương pháp giải:
- Xác định \({S_1}\) là diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = \dfrac{1}{x}\), trục hoành, đường thẳng \(x = \dfrac{1}{2},\,\,x = k\),\({S_2}\) là diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = \dfrac{1}{x}\), trục hoành, đường thẳng \(x = k,\,\,x = 2\).
- Sử dụng công thức: Diện tích hình phẳng phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục hoành, đường thẳng \(x = a,\,\,x = b\) là \(\int\limits_a^b {\left| {f\left( x \right)} \right|dx} \).
- Sử dụng giả thiết \({S_1} = 3{S_2}\) giải phương trình tìm \(k\).
Lời giải chi tiết:
Ta có:
+ \({S_1}\) là diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = \dfrac{1}{x}\), trục hoành, đường thẳng \(x = \dfrac{1}{2},\,\,x = k\), do đó \({S_1} = \int\limits_{\dfrac{1}{2}}^k {\left| {\dfrac{1}{x}} \right|dx} = \int\limits_{\dfrac{1}{2}}^k {\dfrac{1}{x}dx} = \left. {\ln \left| x \right|} \right|_{\dfrac{1}{2}}^k = \ln k - \ln \dfrac{1}{2}\).
+ \({S_2}\) là diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = \dfrac{1}{x}\), trục hoành, đường thẳng \(x = k,\,\,x = 2\), do đó \({S_1} = \int\limits_k^2 {\left| {\dfrac{1}{x}} \right|dx} = \int\limits_k^2 {\dfrac{1}{x}dx} = \left. {\ln \left| x \right|} \right|_k^2 = \ln 2 - \ln k\).
Theo bài ra ta có: \({S_1} = 3{S_2} \Leftrightarrow \ln k - \ln \dfrac{1}{2} = 3\left( {\ln 2 - \ln k} \right)\).
\( \Leftrightarrow \ln k + \ln 2 = 3\ln 2 - 3\ln k\) \( \Leftrightarrow 4\ln k = 2\ln 2 \Leftrightarrow lnk = \dfrac{1}{2}\ln 2 = \ln \sqrt 2 \) \( \Rightarrow k = \sqrt 2 \,\,\left( {tm} \right)\).
Chọn A.







