Câu hỏi
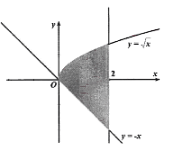
Cho hình phẳng \(D\) giới hạn bởi các đường \(y = \sqrt x ,\)\(y = - x,\)\(x = 2\) (phần tô đậm trong hình). Khối tròn xoay tạo thành khi quay \(D\) quanh trục hoành có thể tích bằng bao nhiêu?
- A \(\left( {\dfrac{{4\sqrt 2 + 6}}{3}} \right)\pi .\)
- B \(\dfrac{2}{3}\pi .\)
- C \(\dfrac{{17}}{6}\pi .\)
- D \(\left( {\dfrac{{14}}{3} + \dfrac{{16\sqrt 2 }}{5}} \right)\pi .\)
Phương pháp giải:
- Tìm hoành độ giao điểm của các hàm số \(y = {x^2} - 2x - 2;y = x + 2\).
- Áp dụng công thức tính thể tích hình phẳng giới hạn bởi các đồ thị hàm số \(y = f\left( x \right)\), \(y = g\left( x \right)\), đường thẳng \(x = a,\,\,x = b\) là: \(V = \pi \int\limits_a^b {\left| {{f^2}\left( x \right) - {g^2}\left( x \right)} \right|dx} \).
Lời giải chi tiết:
Xét phương trình hoành độ giao điểm \(\sqrt x = - x \Leftrightarrow \left\{ \begin{array}{l} - x \ge 0\\x = {x^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \le 0\\\left[ \begin{array}{l}x = 0\\x = 1\end{array} \right.\end{array} \right. \Leftrightarrow x = 0\).
Thể tích khối tròn xoay cần tính là: \(V = \pi \int\limits_0^2 {\left| {x - {x^2}} \right|dx} = \dfrac{{2\pi }}{3}.\)
Chọn B.







