Câu hỏi
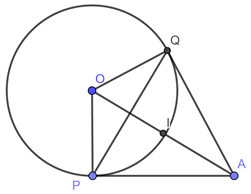
Từ điểm \(A\left( {6;2} \right)\) ta kẻ hai tiếp tuyến với đường tròn \(\left( C \right):{x^2} + {y^2} = 4,\) tiếp xúc với \(\left( C \right)\) lần lượt tại \(P\) và \(Q.\) Tâm \(I\) của đường tròn ngoại tiếp tam giác \(APQ\) có tọa độ là:
- A \(\left( {2;0} \right)\)
- B \(\left( {1;1} \right)\)
- C \(\left( {3;1} \right)\)
- D \(\left( {4;1} \right)\)
Phương pháp giải:
Chứng minh tứ giác \(OQPA\) là tứ giác nội tiếp đường tròn đường kính \(OA \Rightarrow I\) là trung điểm của \(OA.\)
Lời giải chi tiết:
Đường tròn \(\left( C \right):\,\,\,{x^2} + {y^2} = 4\) có tâm \(O\left( {0;0} \right)\) và bán kính \(R = 2.\)
Ta có: \(A\left( {6;\,\,2} \right) \Rightarrow \overrightarrow {OA} = \left( {6;\,\,2} \right) \Rightarrow OA = 2\sqrt {10} > R \Rightarrow \) \(A\left( {6;2} \right)\) nằm ngoài đường tròn.
Lại có: \(I\) là tâm đường tròn ngoại tiếp \(\Delta APQ\) với \(P,\,Q\) là hai tiếp điểm của hai tiếp tuyến kẻ từ \(A\) đến đường tròn \(\left( C \right).\)
Khi đó ta chứng minh được tứ giác \(OPAQ\) là tứ giác nội tiếp.
Lại có: \(\angle OQA = \angle OPA \Rightarrow \) Tâm \(I\) của đường tròn ngoại tiếp tứ giác \(OPAQ\) hay đường tròn ngoại tiếp \(\Delta APQ\) là trung điểm \(OA \Rightarrow \)\(I\left( {3;1} \right)\)
Chọn C.