Phương pháp giải:

Sử dụng công thức: \({d^2} + {r^2} = {R^2}\)

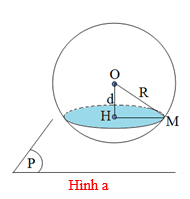
Trong đó, \(d\,\) : khoảng cách từ tâm O đến mặt phẳng (P),

                 \(r\): bán kính đường tròn là giao tuyến của mặt cầu (S) và mặt phẳng (P),

                \(R\): bán kính hình cầu.

Lời giải chi tiết:

Gọi \(R,\,\,r\) lần lượt là bán kính mặt cầu và bán kính đường tròn giao tuyến giữa \(\left( P \right)\) và \(\left( S \right)\).

Ta có: \({S_{cau}} = 4\pi {R^2} = 400\pi \,\,\,\left( {c{m^2}} \right) \Rightarrow r = 10\,\,\,\left( {cm} \right).\)

Gọi \(d = d\left( {O;\left( P \right)} \right) \Rightarrow d = 6\,\,\left( {cm} \right)\).

Ta có: \({d^2} + {r^2} = {R^2} \Rightarrow {6^2} + {r^2} = {10^2} \Rightarrow r = 8\,\,\,\left( {cm} \right).\)

Chọn A.