Lời giải chi tiết:

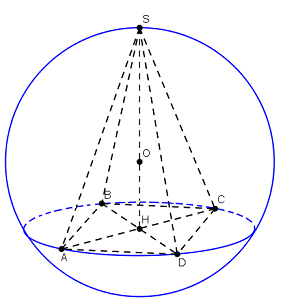
Giả sử  khối chóp đó là S.ABCD. Ta có hình vẽ bên:

Ta có: \(R = \dfrac{{S{A^2}}}{{2.SH}} = 9 \Rightarrow \dfrac{{S{H^2} + A{H^2}}}{{SH}} = 18 \Leftrightarrow A{H^2} = 18.SH - S{H^2}\)

Mặt khác: \({V_{S.ABCD}} = \dfrac{1}{3}.SH.{S_{ABCD}} = \dfrac{1}{3}.SH.\dfrac{{A{C^2}}}{2} = \dfrac{2}{3}.SH.A{H^2} = \dfrac{2}{3}.SH.\left( {18.SH - S{H^2}} \right)\)

Xét hàm số

\(f\left( t \right) = \dfrac{2}{3}{t^2}\left( {18 - t} \right) = \dfrac{8}{3}.\left( {\dfrac{t}{2}.\dfrac{t}{2}.\left( {18 - t} \right)} \right) \le \dfrac{8}{3}{\left( {\dfrac{{t + 18 - t}}{3}} \right)^3} = 576\,\,\left( {0 < t < 18} \right)\)

Dấu “=” xảy ra khi và chỉ khi \(\dfrac{t}{2} = 18 - t \Leftrightarrow t = 12\)

Suy ra, thể tích khối chóp S.ABCD đạt giá trị lớn nhất là 576 khi và chỉ khi \(SH = 12\).

Chọn D.