Câu hỏi
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ sau. Tìm \(m\) để phương trình \(f\left( {\sin x} \right) = m\) có đúng hai nghiệm trên đoạn \(\left[ {0;\pi } \right].\)
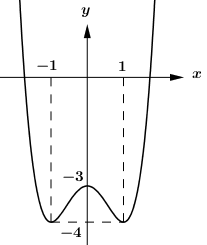
- A \( - 4 < m \le - 3\)
- B \( - 4 \le m \le - 3\)
- C \(m = - 4\) hoặc \(m > - 3\)
- D \( - 4 \le m < - 3\)
Phương pháp giải:
Sử dụng đồ thị.
Lời giải chi tiết:
Đặt \(\sin x = t \in \left[ {0;1} \right]\,\,\,\left( {do\,\,x \in \left[ {0;\pi } \right]} \right)\)\( \Rightarrow t' = \cos x = 0 \Leftrightarrow x = \dfrac{\pi }{2}\)
Bảng biến thiên:
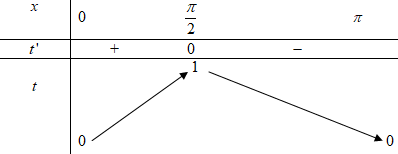
Dựa vào bảng biến thiên ta thấy ứng với mỗi giá trị của t khác 1 thì có 2 giá trị của x.
Do đó để phương trình \(f\left( {\sin x} \right) = m\) có đúng 2 nghiệm trên đoạn \(\left[ {0;2} \right]\) thì phương trình \(f\left( t \right) = m\) phải có một nghiệm duy nhất trên \(\left[ {0;1} \right)\) \( \Rightarrow - 4 < m \le - 3.\)
Chọn A.
Câu hỏi trước
