Phương pháp giải:

- Chứng minh hàm số \(f\left( x \right)\) luôn đồng biến trên \(\mathbb{R}\), đặt \(t = f\left( x \right)\) suy ra với mỗi giá trị của \(t\) cho 1 nghiệm \(x\) tương ứng.

- Đưa bài toán về ẩn \(t\), lập BBT và kết luận.

Lời giải chi tiết:

Xét hàm số \(f\left( x \right) = {x^7} + {x^5} - {x^4} + {x^3} - 2{x^2} + 2x - 10\) ta có:

TXĐ: \(D = \mathbb{R}\).

Ta có: \(f'\left( x \right) = 7{x^6} + 5{x^4} - 4{x^3} + 3{x^2} - 4x + 2\).

Xét hàm số \(h\left( x \right) = 5{x^4} - 4{x^3} + 3{x^2} - 4x + 2\) trên \(\mathbb{R}\) ta có:

\(h'\left( x \right) = 20{x^3} - 12{x^2} + 6x - 4 = 0 \Leftrightarrow x \approx 0,62\).

BBT: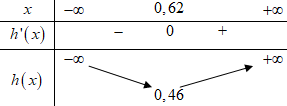

Từ BBT ta thấy \(h\left( x \right) > 0\,\,\forall x \in \mathbb{R}\), do đó \(f'\left( x \right) > 0\,\,\forall x \in \mathbb{R}\).

Đặt \(f\left( x \right) = t\), do hàm số \(f\left( x \right)\) đồng biến trên \(\mathbb{R}\) nên với mỗi giá trị của \(t\) cho ta 1 nghiệm \(x\).

Khi đó \(F\left( t \right) = g\left( t \right) = {t^3} - 3t + 2\).

Yêu cầu bài toán trở thành tìm tham số \(m\) để phương trình \(F\left( t \right) = m\)  có 3 nghiệm \(t\) phân biệt.

Ta có \(g'\left( t \right) = 3{t^2} - 3 = 0 \Leftrightarrow \left[ \begin{array}{l}t = 1\\t =  - 1\end{array} \right.\)

Bảng biến thiên

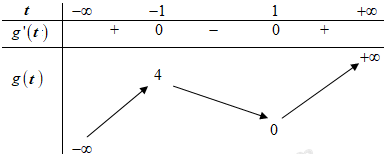
Dựa vào BBT ta thấy phương trình \(F\left( t \right) = m\) có 3 nghiệm phân biệt khi và chỉ khi \(0 < m < 4\).

Chọn B.