Phương pháp giải:

- Cô lập \(m\), đưa phương trình về dạng \(m = f\left( x \right)\). Khi đó số nghiệm của phương trình là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = m\).

- Lập BBT của hàm số \(y = f\left( x \right)\).

- Dựa vào bảng biến thiên để xác định giá trị của m.

Lời giải chi tiết:

Ta có

\(\begin{array}{l}\,\,\,\,\,\,\,\,m\sqrt {{x^2} + 2}  = x + m\\ \Leftrightarrow m\left( {\sqrt {{x^2} + 2}  - 1} \right) = x\\ \Leftrightarrow m = \dfrac{x}{{\sqrt {{x^2} + 2}  - 1}} = f\left( x \right)\,\,\,\left( {x \in \mathbb{R}} \right)\\ \Rightarrow f'\left( x \right) = \dfrac{{2 - \sqrt {{x^2} + 2} }}{{{{\left( {\sqrt {{x^2} + 2}  - 1} \right)}^2}}} = 0 \Leftrightarrow x =  \pm \sqrt 2 \end{array}\)

Bảng biến thiên:

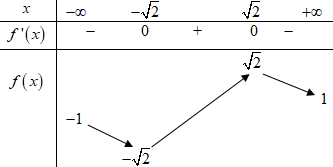
Dựa vào bảng biến thiên ta thấy để hàm số đã cho có 2 nghiệm thì \(\left[ \begin{array}{l} - \sqrt 2  < m <  - 1\\1 < m < \sqrt 2 \end{array} \right.\).

Chọn B.