Môn Toán - Lớp 12
Môn Toán - Lớp 12
 40 bài tập trắc nghiệm giá trị lớn nhất, giá trị nhỏ nhất của hàm số mức độ vận dụng, vận dụng cao
40 bài tập trắc nghiệm giá trị lớn nhất, giá trị nhỏ nhất của hàm số mức độ vận dụng, vận dụng cao
Câu hỏi
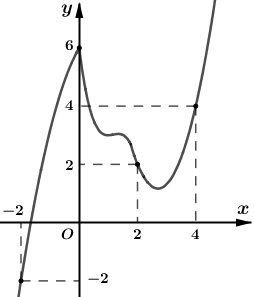
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) có đồ thị \(y = f'\left( x \right)\) như hình vẽ. Đặt \(g\left( x \right) = 2f\left( x \right) - {x^2}\). Khi đó giá trị lớn nhất của hàm số \(g\left( x \right)\) trên đoạn \(\left[ { - 2;4} \right]\) là:
- A \(g\left( { - 2} \right)\).
- B \(g\left( 2 \right)\).
- C \(g\left( 4 \right)\).
- D \(g\left( 0 \right)\).
Phương pháp giải:
- Tính đạo hàm của hàm số \(g\left( x \right)\). Xác định các nghiệm của phương trình \(g'\left( x \right) = 0\).
- Xét dấu \(g'\left( x \right)\) thông qua \(f'\left( x \right)\).
- Lập bảng biến thiên của \(g\left( x \right)\) rồi kết luận giá trị lớn nhất của hàm số trên \(\left[ { - 2;4} \right]\).
Lời giải chi tiết:
Ta có \(g\left( x \right) = 2f\left( x \right) - {x^2}\) \( \Rightarrow g'\left( x \right) = 2f'\left( x \right) - 2x\)
Cho \(g'\left( x \right) = 0 \Leftrightarrow f'\left( x \right) = x\,\,\,\left( 1 \right)\).
Nghiệm của phương trình (1) là hoành độ giao điểm của hai đồ thị hàm số \(y = f'\left( x \right);\,\,y = x.\)
Vẽ đường thẳng \(y = x\) và đồ thị hàm số \(y = f'\left( x \right)\) trên cùng hệ trục tọa độ:
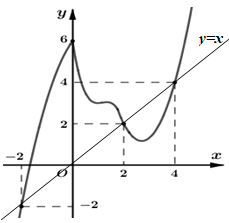
Dựa vào đồ thị ta thấy đồ thị hai hàm số \(y = f'\left( x \right);\,\,y = x\) cắt nhau tại 3 điểm có hoành độ là \( - 2;2;4.\)
\( \Rightarrow g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 2\\x = 2\\x = 4\end{array} \right.\)
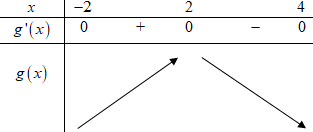
Bảng biến thiên đồ thị hàm số \(y = g\left( x \right)\):
Dựa vào bảng biến thiên ta thấy giá trị lớn nhất của hàm số \(g\left( x \right)\) trên đoạn \(\left[ { - 2;4} \right]\) là \(g\left( 2 \right)\).
Chọn B.